题目内容
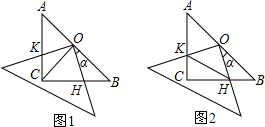
已知:在△ABC中,∠ACB=90°,AC=BC,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O处,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度反(0°<a<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图1所示).那么,在上述旋转过程中:(1)如图1,线段BH与CK具有怎样的数量关系?四边形CHOK的面积是否发生变化?请说明你发现的结论的理由.
(2)如图2,连接HK,
①若AK=12,BH=5,求△OKH的面积;
②若AC=BC=4,设BH=x,当△CKH的面积为2时,求x的值,并说出此时四边形CHOK是什么特殊四边形.
分析:(1)本题关键是要证△OCK≌△OBH,连接CO,因为△ACB是等腰直角三角形,故CO⊥AB,得CO=OB,∠B=∠OCK,及旋转角相等,得出△OCK≌△OBH,故BH=CK,四边形CHOK的面积等于三角形ACB面积的一半.
(2)①由△OCK≌△OBH,得出OK=OH,所以△OKH是等腰直角三角形,所以△OKH的面积=
KH2,求得KH就可求得面积.
②由AC=BC=4,BH=x,可得,CH=4-x,由面积公式可得关于x的方程x2-4x+4=0,解得x=2,又∠KOH=90°,所以四边形CHOK是正方形.
(2)①由△OCK≌△OBH,得出OK=OH,所以△OKH是等腰直角三角形,所以△OKH的面积=
| 1 |
| 4 |
②由AC=BC=4,BH=x,可得,CH=4-x,由面积公式可得关于x的方程x2-4x+4=0,解得x=2,又∠KOH=90°,所以四边形CHOK是正方形.
解答:解:(1)在旋转过程中,BH=CK,四边形CHOK的面积始终保持不变,其值为△ABC面积的一半.
理由如下:连接OC,
∵△ABC为等腰直角三角形,O为斜边AB的中点,CO⊥AB,
∴∠OCK=∠B=45°,CO=OB.
又∵∠COK与∠BOH均为旋转角,
∴∠COK=∠BOH=a,
∴△COK≌△BOH(ASA).
∴BH=CK,S四边形CHOK=S△COK+S△COH=S△BOH+S△COH=S△COB=
S△ABC
(2)①由(1)知,BH=CK=5,AK=CH=12,
在Rt△CKH中,∠C=90°,KH=
=13(KH>0),
∴S△OKH=
OK•OH=
KH2=
.
②由(1)知,CK=BH=x,
∵BC=4,
∴CH=4-x.
∵根据题意,得S△CKH=
CH.CK=2,
(4-x)x=2,
即x2-4x+4=0,
解得x=2(0<x<4).
即CK=CH=BH=2,
∵AC=BC=4,∠A=∠B=45°,
∴CH=BH=2,
∵O为AB中点,
∴OH∥AC,
∴∠OHB=∠C=90°,
∵∠B=45°=∠HOB,
∴OH=BH=2,
同理CK=AK=OK=2,
即CK=OK=KH=CH=2,∠C=90°,
∴四边形CHOK是正方形,
即当△CKH的面积为2时,x的取值是2,此时四边形CHOK是正方形.
理由如下:连接OC,
∵△ABC为等腰直角三角形,O为斜边AB的中点,CO⊥AB,
∴∠OCK=∠B=45°,CO=OB.
又∵∠COK与∠BOH均为旋转角,
∴∠COK=∠BOH=a,
∴△COK≌△BOH(ASA).
∴BH=CK,S四边形CHOK=S△COK+S△COH=S△BOH+S△COH=S△COB=
| 1 |
| 2 |
(2)①由(1)知,BH=CK=5,AK=CH=12,
在Rt△CKH中,∠C=90°,KH=
| 52+122 |
∴S△OKH=
| 1 |
| 2 |
| 1 |
| 4 |
| 169 |
| 4 |
②由(1)知,CK=BH=x,
∵BC=4,
∴CH=4-x.
∵根据题意,得S△CKH=
| 1 |
| 2 |
| 1 |
| 2 |
即x2-4x+4=0,
解得x=2(0<x<4).
即CK=CH=BH=2,
∵AC=BC=4,∠A=∠B=45°,
∴CH=BH=2,
∵O为AB中点,
∴OH∥AC,
∴∠OHB=∠C=90°,
∵∠B=45°=∠HOB,
∴OH=BH=2,
同理CK=AK=OK=2,
即CK=OK=KH=CH=2,∠C=90°,
∴四边形CHOK是正方形,
即当△CKH的面积为2时,x的取值是2,此时四边形CHOK是正方形.
点评:本题考查等腰直角三角形的性质及相关计算,要知道如何判定三角形全等,同学们在解题时,一定要认真观察图象.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
 25、已知:在△ABC中AB=AC,点D在CB的延长线上.
25、已知:在△ABC中AB=AC,点D在CB的延长线上. (1)化简:(a-
(1)化简:(a- 20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长.
20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长. 12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
 已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.
已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.