题目内容
【题目】如图所示,AB是⊙O的直径,弦BC=2cm,∠ABC=60.
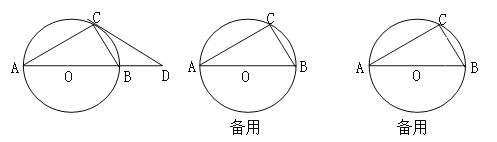
(1)求⊙O的直径;
(2)若D是AB延长线上一点,连结CD,当BD长为多少时,CD与⊙O相切;
(3)若动点E以2cm/s的速度从点A出发沿着AB方向运动,同时动点F以1cm/s的速度从点B出发沿BC方向运动,设运动时间为t(s)(0<t<2),连结EF,当t为何值时,△BEF为直角三角形.
【答案】(1)4cm;(2)2cm;(3)t=1s或t=1.6s时
【解析】试题分析:(1)先根据圆周角定理可得∠ACB=90,再由∠ABC=60可得∠BAC=30,再根据含30°角的直角三角形的性质即可求得结果;
(2)连结OC,根据切线的性质可得∠OCD=90,根据圆周角定理可得∠COD=60,从而可得∠D=30 ,再根据含30°角的直角三角形的性质即可求得结果;
(3)根据题意得BE=(4-2t)cm,BF=tcm,分∠EFB=90与∠FEB=90两种情况结合相似三角形的性质即可求得结果.
(1)∵AB是⊙O的直径
∴∠ACB=90
∵∠ABC=60
∴∠BAC=180-∠ACB-∠ABC=30
∴AB=2BC=4cm,即⊙O的直径为4cm;
(2)如图,连结OC.
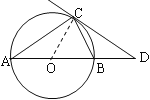
∵CD切⊙O于点C,
∴CD⊥CO
∴∠OCD=90
∵∠BAC=30
∴∠COD=2∠BAC=60.
∴∠D=180-∠COD-∠OCD=30
∴OD=2OC=4cm
∴BD=OD-OB=4-2=2cm
∴当BD长为2cm时,CD与⊙O相切;
(3)根据题意,得BE=(4-2t)cm,BF=tcm;
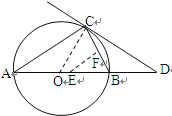
如图,当∠EFB=90时,△BEF为直角三角形,
∵∠EFB=∠ACB,∠B=∠B
∴△BEF∽△BAC
∴![]() ,即
,即![]() ,解得t=1.
,解得t=1.
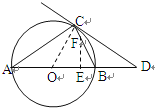
如图,当∠FEB=90时,△BEF为直角三角形,
∵∠FEB=∠ACB,∠B=∠B,
∴△BEF∽△BCA.
∴![]() ,即
,即![]() ,解得t=1.6.
,解得t=1.6.
∴当t=1s或t=1.6s时,△BEF为直角三角形.

 小学教材全测系列答案
小学教材全测系列答案