题目内容
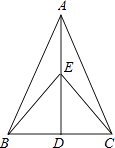
【题目】如图，G，E分别是正方形ABCD的边AB，BC的点，且AG=CE，AE⊥EF，AE=EF，现有如下结论：①BE=
GE；②△AGE≌△ECF；③∠FCD=45°；④△GBE∽△ECH
其中，正确的结论有（ ）
A．1个 B．2个 C．3个 D．4个
【答案】B．
【解析】
试题分析：∵四边形ABCD是正方形，∴∠B=∠DCB=90°，AB=BC，∵AG=CE，∴BG=BE，由勾股定理得：BE=
GE，∴①错误；
∵BG=BE，∠B=90°，∴∠BGE=∠BEG=45°，∴∠AGE=135°，∴∠GAE+∠AEG=45°，∵AE⊥EF，∴∠AEF=90°，∵∠BEG=45°，∴∠AEG+∠FEC=45°，∴∠GAE=∠FEC，在△GAE和△CEF中，∵AG=CE，∠GAE=∠CEF，AE=EF，∴△GAE≌△CEF，∴②正确；
∴∠AGE=∠ECF=135°，∴∠FCD=135°﹣90°=45°，∴③正确；
∵∠BGE=∠BEG=45°，∠AEG+∠FEC=45°，∴∠FEC＜45°，∴△GBE和△ECH不相似，∴④错误；
即正确的有2个．故选B．
练习册系列答案
相关题目
