Question

【题目】如图，在△ABC中，AB=AC，点D是BC的中点，点E在AD上．求证：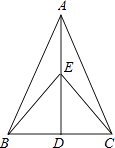
（1）△ABD≌△ACD；
（2）BE=CE．

Answer 1

【答案】
（1）证明：∵D是BC的中点，

∴BD=CD，

在△ABD和△ACD中，

，

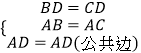∴△ABD≌△ACD（SSS）；

（2）证明：由（1）知△ABD≌△ACD，

∴∠BAD=∠CAD，即∠BAE=∠CAE，

在△ABE和△ACE中，

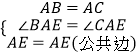
∴△ABE≌△ACE （SAS），

∴BE=CE（全等三角形的对应边相等）

【解析】（1）根据全等三角形的判定定理SSS可以证得△ABD≌△ACD；（2）利用（1）的全等三角形的对应角相等可以推知∠BAE=∠CAE；然后根据全等三角形的判定定理SAS推知△ABE≌△ACE；最后根据全等三角形的对应边相等知BE=CE．
【考点精析】掌握等腰三角形的性质是解答本题的根本，需要知道等腰三角形的两个底角相等（简称：等边对等角）．