Question

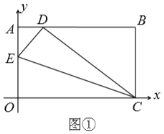
【题目】如图1，在△ABC中，AB＝BC，点D、E分别在边BC，AC上，连接DE，且DE＝DC．

（1）问题发现：若∠ACB＝∠ECD＝45°，则＝　　．

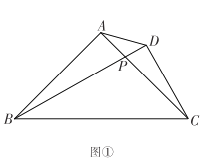
（2）拓展探究：若∠ACB＝∠ECD＝30°，将△EDC饶点C按逆时针旋转α度（0°＜α＜180°），图2是旋转过程中的某一位置，在此过程中的大小有无变化？如果不变，请求出的值，如果变化，请说明理由；

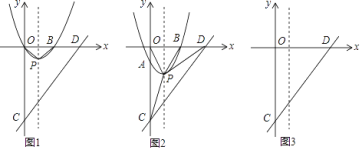
（3）问题解决：若∠ABC＝∠EDC＝β（0°＜β＜90°），将△EDC旋转到如图3所示的位置时，则的值为　　．（用含β的式子表示）

Answer 1

【答案】（1）；（2）不变化，理由详见解析；（3）2cosβ．

【解析】

（1）如图1，过E作EF⊥AB于F，根据等腰三角形的性质得到∠A＝∠C＝∠DEC＝45°，于是得到∠B＝∠EDC＝90°，推出四边形EFBD是矩形，得到EF＝BD，推出△AEF是等腰直角三角形，根据等腰直角三角形的性质得到结论；

（2）根据等腰三角形的性质得到∠ACB＝∠CAB＝∠ECD＝∠CED＝30°，根据相似三角形的判定和性质即可得到结论；

（3）根据等腰三角形的性质得到∠ACB＝∠CAB＝∠ECD＝∠CED＝β，根据相似三角形的性质得到，即，根据角的和差得到∠ACE＝∠BCD，求得△ACE∽△BCD，证得，过点B作BF⊥AC于点F，则AC＝2CF，根据相似三角形的性质即可得到结论．

解：（1）如图1，过E作EF⊥AB于F，

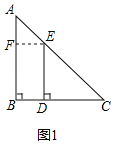
∵BA＝BC，DE＝DC，∠ACB＝∠ECD＝45°，

∴∠A＝∠C＝∠DEC＝45°，

∴∠B＝∠EDC＝90°，

∴四边形EFBD是矩形，

∴EF＝BD，

∴EF∥BC，

∴△AEF是等腰直角三角形，

∴，

故答案为：；

（2）此过程中的大小有变化，

由题意知，△ABC和△EDC都是等腰三角形，

∴∠ACB＝∠CAB＝∠ECD＝∠CED＝30°，

∴△ABC∽△EDC，

∴，即，

又∠ECD+∠ECB＝∠ACB+∠ECB，

∴∠ACE＝∠BCD，

∴△ACE∽△BCD，

∴，

在△ABC中，如图2，过点B作BF⊥AC于点F，

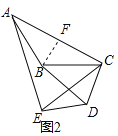
则AC＝2CF，

在Rt△BCF中，CF＝BCcos30°＝BC，

∴AC＝BC．

∴＝；

（3）由题意知，△ABC和△EDC都是等腰三角形，且∠ACB＝∠ECD＝β，

∴∠ACB＝∠CAB＝∠ECD＝∠CED＝β，

∴△ABC∽△EDC，

∴，即，

又∠ECD+∠ECB＝∠ACB+∠ECB，

∴∠ACE＝∠BCD，

∴△ACE∽△BCD，

∴，

在△ABC中，如图3，过点B作BF⊥AC于点F，则AC＝2CF，

在Rt△BCF中，CF＝BCcosβ，

∴AC＝2BCcosβ．

∴＝2cosβ，

故答案为2cosβ．