题目内容
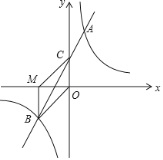
【题目】如图,在平面直角坐标系中,点A、B的坐标分别是A(-1,0)、B(4,5),抛物线![]() +b
+b![]() +c经过A、B两点
+c经过A、B两点
(1)求抛物线的解析式;
(2)点M是线段AB上的一点(不与A、B重合),过M作![]() 轴的垂线交抛物线与点N,求线段MN的最大值,并求出点M、N的坐标;
轴的垂线交抛物线与点N,求线段MN的最大值,并求出点M、N的坐标;
(3)在(2)的条件下,在抛物线上是否存在点P,使得⊿PMN是以MN为直角边的直角三角形?若存在求出点P的坐标,若不存在请说明理由.

【答案】(1)![]() -2
-2![]() -3;(2)MN的最大值为
-3;(2)MN的最大值为![]() ,M、N的坐标分别为M(
,M、N的坐标分别为M(![]() ), N的坐标为N(
), N的坐标为N(![]() ) ;(3)
) ;(3)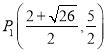 ,
,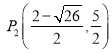 ,
,![]()
【解析】
(1)直接把A、B两点的坐标代入抛物线,即可求出解析式;
(2)先求出直线AB的解析式,然后设点M为(x,x+1),N(![]() ),然后得到MN,结合二次函数的性质,即可求出MN的最大值;
),然后得到MN,结合二次函数的性质,即可求出MN的最大值;
(3)根据题意,可分为:①当以点M为直角三角形的顶点时;②当以点N为直角三角形的顶点时;结合点M、N的纵坐标,即可求出点P的坐标.
解:(1)∵抛物线![]() 经过A(-1,0)、B(4,5)两点,
经过A(-1,0)、B(4,5)两点,
∴![]() ,
,
解得:b=![]() ,c=
,c=![]() ,
,
∴抛物线的解析式:![]() ;
;
(2)∵直线AB经过A(-1,0)、B(4,5)两点,设![]() ,
,
∴得方程组![]() 解得:k=1 ,b=1 ,
解得:k=1 ,b=1 ,
∴直线AB的解析式为![]() ;
;
设M的坐标为M(![]() ), N的坐标为N(
), N的坐标为N(![]() ),
),
MN=![]() ;
;
∴当![]() 时,MN的最大值为
时,MN的最大值为![]() ,
,
∴![]() ,
,![]() ,
,
∴M、N的坐标分别为M(![]() ),N的坐标为N(
),N的坐标为N(![]() ) ;
) ;
(3)在抛物线上是存在点P,使得△PMN是以MN为直角边的直角三角形;
理由如下:如图,
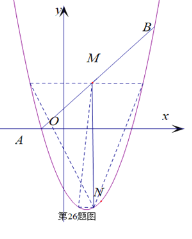
①当以点M为直角三角形的顶点时,![]() ,
,
∴![]() ,
,
解得:![]() =
=![]() ,
,![]() =
=![]() ;
;
②当以点N为直角三角形的顶点时,![]() ,
,
∴![]() ,
,
解得:![]() ,
,![]() =
=![]() (舍去);
(舍去);
∴点P的坐标分别为: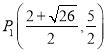 ,
,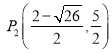 ,
,![]() .
.

练习册系列答案
相关题目