题目内容
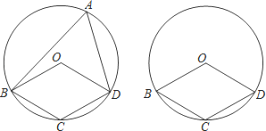
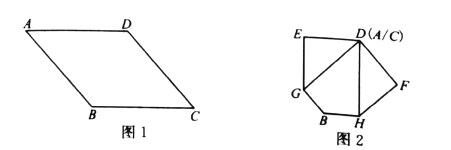
【题目】如图1,菱形纸片![]() ,对其进行如下操作:
,对其进行如下操作:
把![]() 翻折,使得点
翻折,使得点![]() 与点
与点![]() 重,折痕为
重,折痕为![]() ;把
;把![]() 翻折,使得点
翻折,使得点![]() 与点
与点![]() 重合,折痕为
重合,折痕为![]() (如图2),连结
(如图2),连结![]() .设两条折痕的延长线交于点
.设两条折痕的延长线交于点![]() .
.
(1)请在图2中将图形补充完整,并求![]() 的度数;
的度数;
(2)四边形![]() 是菱形吗?说明理由.
是菱形吗?说明理由.
【答案】(1)见解析,![]() ;(2)四边形
;(2)四边形![]() 是菱形,理由见解析
是菱形,理由见解析
【解析】
(1)由菱形的性质可得AD=CD,∠A=∠C=45°,∠ADC=135°,由折叠的性质可得AE=DE=![]() AD,GE⊥AD,∠A=∠GDA=45°,DF=FC=
AD,GE⊥AD,∠A=∠GDA=45°,DF=FC=![]() CD,HF⊥CD,∠C=∠CDH=45°,由四边形的内角和定理可求解;
CD,HF⊥CD,∠C=∠CDH=45°,由四边形的内角和定理可求解;
(2)由题意可证GE∥DH,GD∥HF,可证四边形DGOH是平行四边形,由“ASA”可证△DEG≌△DFH,可得DG=DH,即可证四边形DGOH是菱形.
解:(1)如图,延长EG,FH交于点O,
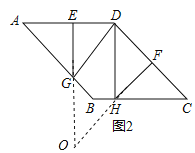
∵四边形ABCD是菱形,∠A=45°,
∴AD=CD,∠A=∠C=45°,∠ADC=135°,
∵把△AEG翻折,使得点A与点D重合,折痕为EG;把△CFH翻折,使得点C与点D重合,折痕为FH,
∴AE=DE=![]() AD,GE⊥AD,∠A=∠GDA=45°,DF=FC=
AD,GE⊥AD,∠A=∠GDA=45°,DF=FC=![]() CD,HF⊥CD,∠C=∠CDH=45°,
CD,HF⊥CD,∠C=∠CDH=45°,
∵∠EOF+∠OED+∠OFD+∠ADC=360°,
∴∠EOF=360°-90°-90°-135°=45°;
(2)四边形![]() 是菱形.理由如下:
是菱形.理由如下:
∵∠ADC=135°,∠ADG=∠CDH=45°,
∴∠GDC=∠ADH=90°,且GE⊥AD,HF⊥CD,
∴GE∥DH,GD∥HF,
∴四边形DGOH是平行四边形,
∵AE=DE=![]() AD,DF=FC=
AD,DF=FC=![]() CD,AD=CD,
CD,AD=CD,
∴DE=DF,且∠ADG=∠CDH=45°,∠DEG=∠DFH=90°,
∴△DEG≌△DFH(ASA)
∴DG=DH,
∴四边形DGOH是菱形.