题目内容
 如图,抛物线m:y=ax2+b(a<0,b>0)与x轴于点A、B(点A在点B的左侧),与y轴交于点C.将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为C1,与x轴的另一个交点为A1.若四边形AC1A1C为矩形,则a,b应满足的关系式为
如图,抛物线m:y=ax2+b(a<0,b>0)与x轴于点A、B(点A在点B的左侧),与y轴交于点C.将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为C1,与x轴的另一个交点为A1.若四边形AC1A1C为矩形,则a,b应满足的关系式为
- A.ab=-2
- B.ab=-3
- C.ab=-4
- D.ab=-5
B
分析:假设a=-1,b=1得出抛物线m的解析式,再利用C与C1关于点B中心对称,得出二次函数的顶点坐标,利用矩形性质得出要使平行四边形AC1A1C是矩形,必须满足AB=BC,即可求出.
解答:假设a=-1,b=1时,抛物线m的解析式为:y=-x2+1.
令x=0,得:y=1.∴C(0,1).
令y=0,得:x=±1.
∴A(-1,0),B(1,0),
∵C与C1关于点B中心对称,
∴抛物线n的解析式为:y=(x-2)2-1=x2-4x+3;
令x=0,得:y=b.∴C(0,b).
令y=0,得:ax2+b=0,∴x=± ,∴A(-
,∴A(- ,0),B(
,0),B( ,0),
,0),
∴AB=2 ,BC=
,BC= =
=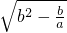 .
.
要使平行四边形AC1A1C是矩形,必须满足AB=BC,
∴2 =
=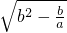 .∴4×(-
.∴4×(- )=b2-
)=b2- ,
,
∴ab=-3.
∴a,b应满足关系式ab=-3.
故选B.
点评:此题主要考查了平行四边形的性质以及矩形的性质和点的坐标关于一点中心对称的性质,灵活应用平行四边形的性质是解决问题的关键.
分析:假设a=-1,b=1得出抛物线m的解析式,再利用C与C1关于点B中心对称,得出二次函数的顶点坐标,利用矩形性质得出要使平行四边形AC1A1C是矩形,必须满足AB=BC,即可求出.
解答:假设a=-1,b=1时,抛物线m的解析式为:y=-x2+1.
令x=0,得:y=1.∴C(0,1).
令y=0,得:x=±1.
∴A(-1,0),B(1,0),
∵C与C1关于点B中心对称,
∴抛物线n的解析式为:y=(x-2)2-1=x2-4x+3;
令x=0,得:y=b.∴C(0,b).
令y=0,得:ax2+b=0,∴x=±
 ,∴A(-
,∴A(- ,0),B(
,0),B( ,0),
,0),∴AB=2
 ,BC=
,BC= =
=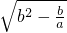 .
.要使平行四边形AC1A1C是矩形,必须满足AB=BC,
∴2
 =
=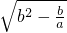 .∴4×(-
.∴4×(- )=b2-
)=b2- ,
,∴ab=-3.
∴a,b应满足关系式ab=-3.
故选B.
点评:此题主要考查了平行四边形的性质以及矩形的性质和点的坐标关于一点中心对称的性质,灵活应用平行四边形的性质是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
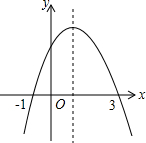 如图,抛物线y=ax2+bx+c(a≠0)与x轴两交点是A(-1,0),B(3,0),则如图可知y<0时,x的取值范围是( )
如图,抛物线y=ax2+bx+c(a≠0)与x轴两交点是A(-1,0),B(3,0),则如图可知y<0时,x的取值范围是( )| A、-1<x<3 | B、3<x<-1 | C、x>-1或x<3 | D、x<-1或x>3 |
 26、已知:如图,抛物线C1,C2关于x轴对称;抛物线C1,C3关于y轴对称.抛物线C1,C2,C3与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线C1,C2,C3的顶点.HN垂直于x轴,垂足为N,且|OE|>|HN|,|AB|≠|HG|
26、已知:如图,抛物线C1,C2关于x轴对称;抛物线C1,C3关于y轴对称.抛物线C1,C2,C3与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线C1,C2,C3的顶点.HN垂直于x轴,垂足为N,且|OE|>|HN|,|AB|≠|HG|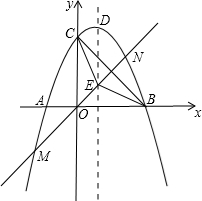 如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4).
如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4).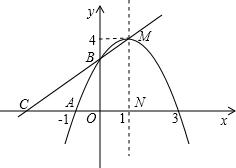 以P为圆心的圆经过点A,并且与直线BM相切?若存在,求出点P的坐标;若不存在,请说明理由.
以P为圆心的圆经过点A,并且与直线BM相切?若存在,求出点P的坐标;若不存在,请说明理由.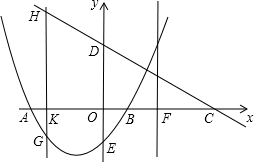 .点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行.直线y=-x+m过点C,交y轴于D点.
.点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行.直线y=-x+m过点C,交y轴于D点.