题目内容
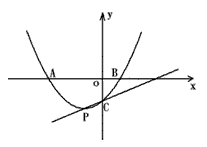
 如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4).
如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4).(1)求抛物线的解析式,并写出顶点D的坐标;
(2)若直线y=x交抛物线于M,N两点,交抛物线的对称轴于点E,连接BC,EB,EC.试判断△EBC的形状,并加以证明;
(3)设P为直线MN上的动点,过P作PF∥ED交直线MN上方的抛物线于点F.问:在直线MN上是否存在点P,使得以P,E,D,F为顶点的四边形是平行四边形?若存在,请求出点P及相应的点F的坐标;若不存在,请说明理由.
分析:(1)设抛物线的解析式是:y=a(x+2)(x-4),将(0,4)代入,求出a=-
,即可得到抛物线的解析式,把解析式化成顶点式即可求出顶点坐标;
(2)△EBC应为钝角三角形.根据直线MN⊥BC于直线点Q,求出tan∠EBQ=
,得出∠EBQ<45°即可;
(3)存在.设点P的坐标为点(x0,y0)(x0=y0),只要PF∥ED,PF=ED,根据点F在抛物线上,求出|YF-Y0|=DE=
,求出x0=-1,即可得到点P的坐标和点F的坐标.
| 1 |
| 2 |
(2)△EBC应为钝角三角形.根据直线MN⊥BC于直线点Q,求出tan∠EBQ=
| 1 |
| 2 |
(3)存在.设点P的坐标为点(x0,y0)(x0=y0),只要PF∥ED,PF=ED,根据点F在抛物线上,求出|YF-Y0|=DE=
| 7 |
| 2 |
解答:解:(1)设抛物线的解析式是:y=a(x+2)(x-4),
将(0,4)代入,得a=-
,
∴y=-
x2+x+4,
∴y=-
(x2-2x-8)=-
(x-1)2+
,顶点D为(1,
);
答:抛物线的解析式是y=-
x2+x+4,顶点D的坐标是(1,
).
(2)答:△EBC应为钝角三角形.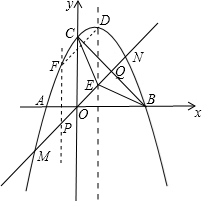
证明:∵直线MN⊥BC于直线点Q,
在直角三角形EBQ中,tan∠EBQ=
,
∴∠EBQ<45°,
可得∠BEC为钝角,
∴△EBC应为钝角三角形.
∵△OEC≌△OEB,
∴EB=EC,
∴△EBC也是等腰三角形.
(3)解:存在.
设点P的坐标为点(x0,y0)(x0=y0),
∵PF∥ED,
∴只需使得PF=ED,
∵点F在抛物线上,
∴yF=-
+x0+4,|yF-y0| =-
+4=|ED| =
,
可解得x0=±1,取x0=-1,
则存在点P的坐标为(-1,-1),点F的坐标为(-1,
),符合题目的条件,
答:存在,点P的坐标为(-1,-1),点F的坐标为(-1,
).
将(0,4)代入,得a=-
| 1 |
| 2 |
∴y=-
| 1 |
| 2 |
∴y=-
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
答:抛物线的解析式是y=-
| 1 |
| 2 |
| 9 |
| 2 |
(2)答:△EBC应为钝角三角形.

证明:∵直线MN⊥BC于直线点Q,
在直角三角形EBQ中,tan∠EBQ=
| 1 |
| 2 |
∴∠EBQ<45°,
可得∠BEC为钝角,
∴△EBC应为钝角三角形.
∵△OEC≌△OEB,
∴EB=EC,
∴△EBC也是等腰三角形.
(3)解:存在.
设点P的坐标为点(x0,y0)(x0=y0),
∵PF∥ED,
∴只需使得PF=ED,
∵点F在抛物线上,
∴yF=-
| 1 |
| 2 |
| x | 2 0 |
| 1 |
| 2 |
| x | 2 0 |
| 7 |
| 2 |
可解得x0=±1,取x0=-1,
则存在点P的坐标为(-1,-1),点F的坐标为(-1,
| 5 |
| 2 |
答:存在,点P的坐标为(-1,-1),点F的坐标为(-1,
| 5 |
| 2 |
点评:本题主要考查对用待定系数法求二次函数的解析式,锐角三角函数的定义,解一元二次方程等知识点的理解和掌握,综合运用性质进行计算是解此题的关键,题目比较典型,难度适中.

练习册系列答案
相关题目
 如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,-4).
如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,-4).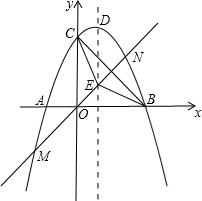 如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4).
如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4).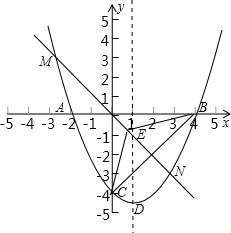 请说明理由.
请说明理由. 交x轴于A、B两点,交y轴于点C,点P是它的顶点,点A的横坐标是-3,点B的横坐标是1。
交x轴于A、B两点,交y轴于点C,点P是它的顶点,点A的横坐标是-3,点B的横坐标是1。 ,
, ,
, )
)