题目内容
 26、已知:如图,抛物线C1,C2关于x轴对称;抛物线C1,C3关于y轴对称.抛物线C1,C2,C3与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线C1,C2,C3的顶点.HN垂直于x轴,垂足为N,且|OE|>|HN|,|AB|≠|HG|
26、已知:如图,抛物线C1,C2关于x轴对称;抛物线C1,C3关于y轴对称.抛物线C1,C2,C3与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线C1,C2,C3的顶点.HN垂直于x轴,垂足为N,且|OE|>|HN|,|AB|≠|HG|(1)A、B、C、D、E、F、G、H、M9个点中,四个点可以连接成一个四边形,请你用字母写出下列特殊四边形:菱形
AHBG
;等腰梯形HGEF
;平行四边形EGFM
;梯形DMHC
;(每种特殊四边形只能写一个,写错、多写记0分)(2)证明其中任意一个特殊四边形;
(3)写出你证明的特殊四边形的性质.
分析:(1)结合图形和题意,四边形AHBG四条边相等且对角线互相垂直是菱形,四边形HGEF符合等腰图形的特征,四边形EGFM对角线互相平分是平行四边形,四边形DMHC只有一组对边平行,所以是梯形;
(2)证明EBFC为菱形,证明四条边相等且对角线互相垂直即可;(3)从边、对角线、角等几方面说明特殊四边形的性质.
(2)证明EBFC为菱形,证明四条边相等且对角线互相垂直即可;(3)从边、对角线、角等几方面说明特殊四边形的性质.
解答:解:(1)菱形:AHBG,EBFC,AFDE(1分)
等腰梯形:HGEF,BCMH,AHMD(2分)
梯形:DMHC,MHAB(3分)
平行四边形:EGFM,AHMC,MHBD,AGDM.(4分)
(2)在四边形EBFC中,
∵c1,c2关于y轴对称
∴OC=OB(5分)
∵C1,C2关于x轴对称
∴OE=OF(6分)
又EF⊥OB.
∴EBFC为菱形(8分)
(3)菱形的性质有:①四条边相等;
②对角线互相垂直平分;
③每一条对角线平分一组对角;
④对角相等.(12分)
等腰梯形:HGEF,BCMH,AHMD(2分)
梯形:DMHC,MHAB(3分)
平行四边形:EGFM,AHMC,MHBD,AGDM.(4分)
(2)在四边形EBFC中,
∵c1,c2关于y轴对称
∴OC=OB(5分)
∵C1,C2关于x轴对称
∴OE=OF(6分)
又EF⊥OB.
∴EBFC为菱形(8分)
(3)菱形的性质有:①四条边相等;
②对角线互相垂直平分;
③每一条对角线平分一组对角;
④对角相等.(12分)
点评:本题考查的是菱形,等腰梯形,平行四边形的判定以及菱形的性质.考生要学会看二次函数的图象,本题难度不大.

练习册系列答案
相关题目
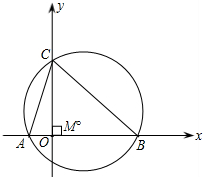 与y轴交点C的纵坐标为3,△ABC的外接圆的圆心为点M.
与y轴交点C的纵坐标为3,△ABC的外接圆的圆心为点M. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, (2013•宁化县质检)已知:如图,抛物线y=ax2+bx+c与x轴交于点A(
(2013•宁化县质检)已知:如图,抛物线y=ax2+bx+c与x轴交于点A( 已知,如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A,B,点A的坐标为(4,0).
已知,如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A,B,点A的坐标为(4,0). 已知,如图,抛物线y=x2+px+q与x轴相交于A、B两点,与y轴交于点C,且OA≠OB,OA=OC,设抛物线的顶点为点P,直线PC与x轴的交点D恰好与点A关于y轴对称.
已知,如图,抛物线y=x2+px+q与x轴相交于A、B两点,与y轴交于点C,且OA≠OB,OA=OC,设抛物线的顶点为点P,直线PC与x轴的交点D恰好与点A关于y轴对称.