��Ŀ����
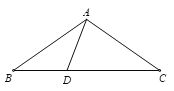
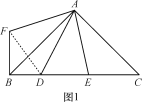
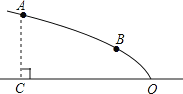
����Ŀ����ͼ��ij�㳡��Ƶ�һ���������͵��ݽ����������ߵ�һ���֣������ߵĶ���O����ˮƽ���ϣ��Գ�����ˮƽ��OC����A��B�������������ϣ��ҵ�A��ˮƽ��ľ���AC=4�ף���B��ˮƽ�����Ϊ2�ף�OC=8�ף�
��1���뽨���ʵ���ֱ������ϵ���������ߵĺ�������ʽ��
��2��Ϊ�˰�ȫ���ۣ�������ˮƽ��OC����һ��P�����ʵء������ȷ����Բ�θֹ���������֧��PA��PB�����������ͽ���֧�żӹ̣���ô���������ҵ�����֧��������ʡ��֧������桢���ͶԽӷ�ʽ�����϶��������ݲ����ǣ�ʱ�ĵ�P��������֤����
��3��Ϊ��ʩ�����㣬����������O��P֮��ľ��룬��ô����֧��������ʡʱ��O��P֮��ľ����Ƕ��٣�����д�����̣�
���𰸡���1�������ߵĺ�������ʽΪ��y=![]() x2��
x2��
��2���ҷ�������
��3������֧��������ʡʱ����O��P֮��ľ�����4�ף�
��������
��1������������Խ������ʵ�ƽ��ֱ������ϵ���Ӷ�������������ߵĽ���ʽ��
��2����������֮���߶���࣬������Ӧ��ͼ�Σ�д���������ɣ�
��3������ǰ�������ϵ�������߽���ʽ������õ�B�����꣬�ٸ������������ƿ����������֧��������ʡʱ��O��P֮��ľ��룬ע��˴�ֻд���𰸼��ɣ�
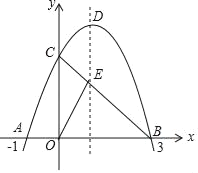
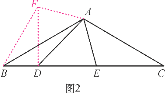
�⣺��1����ͼ��
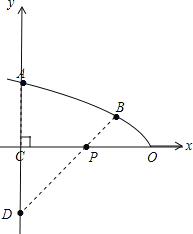
�Ե�OΪԭ�㡢����OCΪy��������Ὠ��ֱ������ϵ��
�������ߵĺ�������ʽΪy=ax2��
������֪��A������Ϊ��4��8����
�ߵ�A���������ϣ�
��8=a��42��
���a=![]() ��
��
�����������ߵĺ�������ʽΪ��y=![]() x2��
x2��
��2���ҷ���
�ӳ�AC�������������������������ڵ�D��
���A��D����OC�Գƣ�
����BD��OC�ڵ�P�����P��Ϊ����
��3������ͼ��������֪��B�ĺ�����Ϊ2��
�ߵ�B���������ϣ�
���B��������2��2����
�֡ߵ�A������Ϊ��4��8����
���D����������4��8����
��ֱ��BD�ĺ�������ʽΪy=kx+b��
��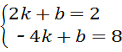 ��
��
��ã�k=��1��b=4��
��ֱ��BD�ĺ�������ʽΪy=��x+4��
��x=0����y=��x+4���õ�P������Ϊ��0��4����
����֧��������ʡʱ����O��P֮��ľ�����4�ף�