题目内容
(本小题满分5分)
已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC、AC于点D、E,联结EB交OD于点F.
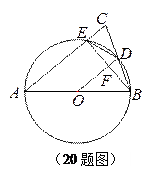
(1)求证:OD⊥BE;
(2)若DE= ,AB=5,求AE的长.
,AB=5,求AE的长.
已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC、AC于点D、E,联结EB交OD于点F.

(1)求证:OD⊥BE;
(2)若DE=
 ,AB=5,求AE的长.
,AB=5,求AE的长.解:(1)联结AD
∵AB是⊙O的直径,∴∠ADB=∠AEB =90° --- 1分
∵AB=AC,∴CD=BD
∵OA=OB,∴OD//AC
∴OD⊥BE --------------------------------------- 2分
(2)方法一:∵∠CEB=∠AEB=90°,CD="BD,AB=5," DE=
∴AC="AB=5, " BC=2DE=2 , --------------------- 3分
, --------------------- 3分
在△ABE、△BCE中,∠CEB=∠AEB=90°,则有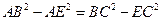
设AE="x," 则 --------------------- 4分
--------------------- 4分
解得:x="3 "
∴AE="3 " -------------------------- 5分
方法二:∵OD⊥BE,∴BD=DE,BF="EF " ------------------------3分
设AE=x,∴OF= ,在△OBF、△BDF中,∠OFB=∠BFD=90°
,在△OBF、△BDF中,∠OFB=∠BFD=90°
∴
∵DE= ,AB=5, ∴
,AB=5, ∴ ------4分
------4分
解得:x=3, ∴AE="3 " ------------5分
方法三:∵BE⊥AC AD⊥BC,
∴S△ABC=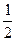 BC·AD=
BC·AD=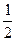 AC·BE, ----------------------------3分
AC·BE, ----------------------------3分
∴BC·AD=AC·BE
∵BC=2DE=2 ,AC=AB=5
,AC=AB=5
∴BE="4" , ----------------------------------4分
∴AE="3 " ------------------------------5分
∵AB是⊙O的直径,∴∠ADB=∠AEB =90° --- 1分
∵AB=AC,∴CD=BD
∵OA=OB,∴OD//AC
∴OD⊥BE --------------------------------------- 2分
(2)方法一:∵∠CEB=∠AEB=90°,CD="BD,AB=5," DE=

∴AC="AB=5, " BC=2DE=2
 , --------------------- 3分
, --------------------- 3分在△ABE、△BCE中,∠CEB=∠AEB=90°,则有
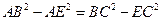
设AE="x," 则
 --------------------- 4分
--------------------- 4分解得:x="3 "
∴AE="3 " -------------------------- 5分
方法二:∵OD⊥BE,∴BD=DE,BF="EF " ------------------------3分
设AE=x,∴OF=
 ,在△OBF、△BDF中,∠OFB=∠BFD=90°
,在△OBF、△BDF中,∠OFB=∠BFD=90°∴

∵DE=
 ,AB=5, ∴
,AB=5, ∴ ------4分
------4分解得:x=3, ∴AE="3 " ------------5分
方法三:∵BE⊥AC AD⊥BC,
∴S△ABC=
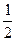 BC·AD=
BC·AD=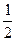 AC·BE, ----------------------------3分
AC·BE, ----------------------------3分∴BC·AD=AC·BE
∵BC=2DE=2
 ,AC=AB=5
,AC=AB=5∴BE="4" , ----------------------------------4分
∴AE="3 " ------------------------------5分
略

练习册系列答案
相关题目
 ,垂足为D,若
,垂足为D,若 ,
, ,求DE的长.
,求DE的长.
 ,则a的值是( )
,则a的值是( )

 ,求OD的长度.
,求OD的长度.

 )
) 

