题目内容
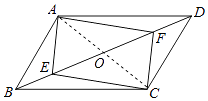
【题目】如图：在ABCD中，E、F分别为对角线BD上的点，且BE=DF，判断四边形AECF的形状，并说明理由． 
【答案】证明：连接AC，与BD相交于O，如图所示：
∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD，
∵BE=DF，
∴OE=OF，
∴AC与EF互相平分，
∴四边形AECF为平行四边形；
【解析】在平行四边形ABCD中，AC与BD互相平分，OA=OC，OB=OD，又BE=DF，得出OE=OF，得出AC与EF互相平分，证出四边形AECF为平行四边形．
【考点精析】本题主要考查了平行四边形的性质的相关知识点，需要掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分才能正确解答此题．
练习册系列答案
轻松课堂单元测试AB卷系列答案
小题狂做系列答案
相关题目
【题目】观察下表三行数的规律，回答下列问题：
第1列 | 第2列 | 第3列 | 第4列 | 第5列 | 第6列 | … | |
第1行 | -2 | 4 | -8 | a | -32 | 64 | … |
第2行 | 0 | 6 | -6 | 18 | -30 | 66 | … |
第3行 | -1 | 2 | -4 | 8 | -16 | b | … |
（1）第1行的第四个数a是 ；第3行的第六个数b是 ；
（2）若第1行的某一列的数为c，则第2行与它同一列的数为 ；
（3）已知第n列的三个数的和为2562，若设第1行第n列的数为x，试求x的值．
