题目内容
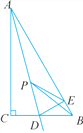
【题目】如图所示,∠1=∠2,AE⊥OB于E,BD⊥OA于D,交点为C,则图中全等三角形共有( )

A. 2对 B. 3对 C. 4对 D. 5对
【答案】C
【解析】试题分析:根据已知条件可以找出题目中有哪些相等的角以及线段,然后猜想可能全等的三角形,然后一一进行验证,做题时要由易到难,循序渐进.
解:①△ODC≌△OEC,
∵BD⊥AO于点D,AE⊥OB于点E,OC平分∠AOB,
∴∠ODC=∠OEC=90°,∠1=∠2,
∵OC=OC,
∴△ODC≌△OEC(AAS),
∴OE=OD,CD=CE;
②△ADC≌△BEC,
∵∠CDA=∠CEB=90°,∠3=∠4,CD=CE,
∴△ADC≌△BEC(ASA),
∴AC=BC,AD=BE,∠B=∠A;
③△OAC≌△OBC,
∵OD=OE,
∴OA=OB,
∵OA=OB,OC=OC,AC=BC,
∴△OAC≌△OBC(SSS);
④△OAE≌△OBD,
∵∠ODB=∠OEA=90°,OA=OB,OD=OE,
∴△OAE≌△OBD(HL).
故选C.

练习册系列答案
相关题目