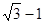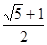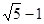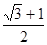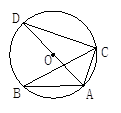题目内容
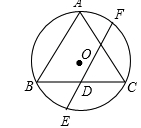
如图,已知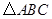 ,以
,以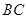 为直径,
为直径,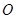 为圆心的半圆交
为圆心的半圆交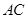 于点
于点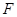 ,点
,点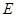 为弧CF的中点,连接
为弧CF的中点,连接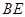 交
交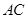 于点
于点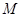 ,
, 为△ABC的角平分线,且
为△ABC的角平分线,且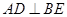 ,垂足为点
,垂足为点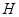 .
.
小题1:求证: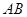 是半圆
是半圆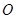 的切线;
的切线;
小题2:若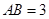 ,
,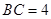 ,求
,求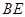 的长.
的长.
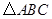 ,以
,以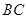 为直径,
为直径,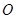 为圆心的半圆交
为圆心的半圆交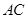 于点
于点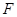 ,点
,点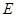 为弧CF的中点,连接
为弧CF的中点,连接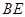 交
交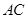 于点
于点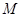 ,
, 为△ABC的角平分线,且
为△ABC的角平分线,且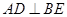 ,垂足为点
,垂足为点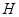 .
.小题1:求证:
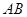 是半圆
是半圆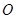 的切线;
的切线;小题2:若
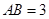 ,
,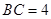 ,求
,求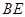 的长.
的长.
小题1:证明:连接EC,
∵AD⊥BE于H,∠1=∠2,
∴∠3=∠4 ∴∠4=∠5=∠3,
又∵E为弧CF中点, ∴∠6=∠7,
∵BC是直径, ∴∠E=90°, ∴∠5+∠6=90°,
又∵∠AHM=∠E=90°, ∴AD∥CE,
∴∠2=∠6=∠1, ∴∠3+∠7=90°,
又∵BC是直径, ∴AB是半圆O的切线;
小题2:∵
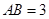 ,
,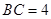 。
。由(1)知,
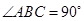 ,∴
,∴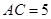 .
.在
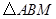 中,
中,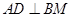 于
于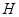 ,
, 平分
平分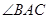 ,
,∴
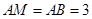 ,∴
,∴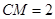 .
. 由
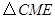 ∽
∽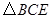 ,得
,得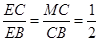 .
.∴
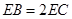 ,
,∴
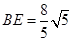
略

练习册系列答案
相关题目
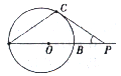
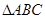 是⊙O的内接正三角形,弦
是⊙O的内接正三角形,弦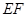 经过
经过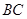 边的中点
边的中点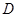 ,且
,且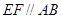 ,若⊙O的半径为
,若⊙O的半径为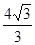 ,则
,则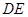 的长为( )
的长为( )