题目内容
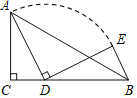
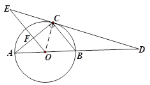
【题目】如图,⊙![]() 为
为![]() 的外接圆,
的外接圆,![]() ,过点
,过点![]() 的切线与
的切线与![]() 的延长线交于点
的延长线交于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() .
.
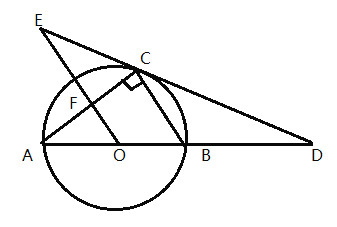
(1)判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若![]() ,求
,求![]() 的长.
的长.
【答案】(1)OE∥BC.理由见解析;(2)![]()
【解析】
(1)连接OC,根据已知条件可推出![]() ,进一步得出
,进一步得出![]() 结论得以证明;
结论得以证明;
(2)根据(1)的结论可得出∠E=∠BCD,对应的正切值相等,可得出CE的值,进一步计算出OE的值,在Rt△AFO中,设OF=3x,则AF=4x,解出x的值,继而得出OF的值,从而可得出答案.
解:(1) OE∥BC.理由如下:
连接OC,
∵CD是⊙O的切线,
∴OC⊥CD,
∴∠OCE=90![]() ,
,
∴∠OCA+∠ECF=90![]() ,
,
∵OC=OA,
∴∠OCA=∠CAB.
又∵∠CAB=∠E,
∴∠OCA=∠E,
∴∠E+∠ECF=90![]() ,
,
∴∠EFC=180O-(∠E+∠ECF) =90![]() .
.
∴∠EFC=∠ACB=90![]() ,
,
∴OE∥BC.
(2)由(1)知,OE∥BC,
∴∠E=∠BCD.
在Rt△OCE中,∵AB=12,
∴OC=6,
∵tanE=tan∠BCD=![]() ,
,
∴![]() .
.
∴OE2=OC2+CE2=62+82,
∴OE=10
又由(1)知∠EFC =90![]() ,
,
∴∠AFO=90![]() .
.
在Rt△AFO中,∵tanA =tanE=![]() ,
,
∴设OF=3x,则AF=4x.
∵OA2=OF2+AF2,即62=(3x)2+(4x)2,
解得:![]()
∴![]() ,
,
∴![]() .
.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目