题目内容
【题目】在矩形ABCD中,AB=4,AD=8.
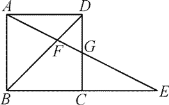
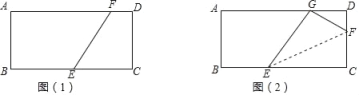
(1)如图①若E从B到C运动,F从D到A运动且BE=2DF,
( i)当DF为何值时四边形ECDF是矩形.
( ii)当DF为何值时EF=2![]() .
.
(2)如图②E在BC上,BE=3,F在CD上,将△ECF沿EF折叠,当C点恰好落在AD边上的G处时,求折痕EF的长.
【答案】(1)(i)DF=![]() ;(ii)DF=2或
;(ii)DF=2或![]() ;(2)EF=
;(2)EF=![]() .
.
【解析】
(1)(i)设DF=m,BE=2m,则EC=8﹣2m,由矩形的性质可得DF=EC,由此可得方程m=8﹣2m,解方程即可求得m的值;(ii)分点E在点F的左边和点F在点E的左边两种情况求解;(2)过E作EH⊥AD于H,即可得BE=AH=3,EC=5,由折叠的性质可得EG=EC=5,GF=CF,由勾股定理求得HG=3,即可得GD=2,设GF=FC=x,则DF=4﹣x,在Rt△GDF中,根据勾股定理可得22+(4﹣x)2=x2,解方程求得x的值,即可得FC的长,再利用勾股定理求得EF的长即可.
(1)(i)设DF=m,BE=2m,则EC=8﹣2m,
由矩形的性质:DF=EC,
∴m=8﹣2m
∴![]()
∴![]() ;
;
( ii)如图(1)过F作FM⊥BC于M,
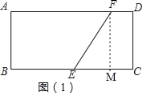
∴FM=AB=4,EF=![]() ,
,
∴勾股定理得![]() ,
,
∴BM+MC=2m+2+m=8,
∴m=2;
如图(2)过E作FN⊥BC于N,
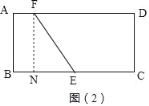
同理可得NE=2,
∴BN+NC=2m﹣2+m=8,m=![]() ,
,
∴DF=2或![]() ;
;
(2)过E作EH⊥AD于H,
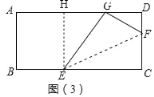
∵BE=AH=3,
∴EC=5,
由折叠的性质EG=EC=5,GF=CF,
∵HE=AB=4,
∴![]() ,
,
∴GD=AD﹣AH﹣HG=2,
设GF=FC=x,则DF=4﹣x,
在Rt△GDF中,GD2+DF2=GF2
∴22+(4﹣x)2=x2
解得![]() ,即
,即![]() ,
,
∴![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】为了让同学们了解自己的体育水平,初二1班的体育刘老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
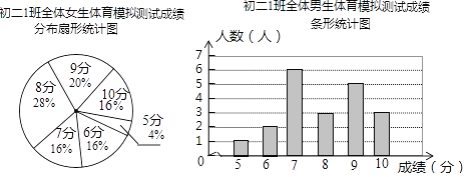
初二1班体育模拟测试成绩分析表
平均分 | 方差 | 中位数 | 众数 | |
男生 | 2 | 8 | 7 | |
女生 | 7.92 | 1.99 | 8 |
根据以上信息,解答下列问题:
(1)这个班共有男生________人,共有女生________人;
(2)补全初二1班体育模拟测试成绩分析表.