Question

【题目】如图，等腰△ABC内接于半径为5的⊙O，AB＝AC，tan∠ABC＝．求BC的长．

Answer 1

【答案】BC＝6．

【解析】

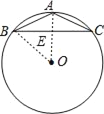
连接AO，交BC于点E，连接BO，求出，根据垂径定理得出OA⊥BC，BC＝2BE，设AE＝x，则BE＝3x，OE＝5﹣x，根据勾股定理得出方程（3x）2+（5﹣x）2＝52，求出方程的解即可．

连接AO，交BC于点E，连接BO，

∵AB＝AC，

∴，

又∵OA是半径，

∴OA⊥BC，BC＝2BE，

在Rt△ABE中，∵tan∠ABC＝，

∴，

设AE＝x，则BE＝3x，OE＝5﹣x，

在Rt△BEO中，BE2+OE2＝OB2，

∴(3x)2+(5﹣x)2＝52，

解得：x1＝0(舍去)，x2＝1，

∴BE＝3x＝3，

∴BC＝2BE＝6．