题目内容
如图1,直线AB的解析式为y=kx-6,且分式
=0,以A点为顶点在第四象限做等腰直角三角形△ABC.

(1)求A点和C点的坐标.
(2)在第四象限是否存在一点P,使△PBA≌CAB?若存在,求出P点坐标;若不存在,说明理由.
(3)如图2,Q为y轴负半轴上一个动点,当Q点向y轴负半轴向下运动时,以Q为顶点,在第三象限作等腰直角三角形△ADQ,过D作DE⊥x轴于E点,下列两个结论:①OQ-DE的值不变,②OQ+DE的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,说出你的理由并求出其值.
| k-2 | k-3 |

(1)求A点和C点的坐标.
(2)在第四象限是否存在一点P,使△PBA≌CAB?若存在,求出P点坐标;若不存在,说明理由.
(3)如图2,Q为y轴负半轴上一个动点,当Q点向y轴负半轴向下运动时,以Q为顶点,在第三象限作等腰直角三角形△ADQ,过D作DE⊥x轴于E点,下列两个结论:①OQ-DE的值不变,②OQ+DE的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,说出你的理由并求出其值.
分析:(1)求出k,分别把x=0和y=0代入一次函数的解析式,求出A、B的坐标,求出OA、OB值,证△OBA≌△EAC,推出CE=OA=3,AE=OB=6,即可求出C的坐标;
(2)过P作PQ⊥y轴于Q,证出△PQB≌△BOA,推出BQ=OA=3,PQ=OB=6,求出OQ=9,即可得出P的坐标;
(3)过D作DF⊥y轴于F,求出∠FDQ=∠FQA,根据AAS证△DFQ≌△AOQ,推出FQ=AO=3,推出四边形DEOF是矩形,得到DE=OF,即可求出OQ-DE=FQ=3,得出答案即可.
(2)过P作PQ⊥y轴于Q,证出△PQB≌△BOA,推出BQ=OA=3,PQ=OB=6,求出OQ=9,即可得出P的坐标;
(3)过D作DF⊥y轴于F,求出∠FDQ=∠FQA,根据AAS证△DFQ≌△AOQ,推出FQ=AO=3,推出四边形DEOF是矩形,得到DE=OF,即可求出OQ-DE=FQ=3,得出答案即可.
解答: (1)解:∵
(1)解:∵
=0,
∴k-2=0,
∴k=2,
∴y=2x-6,
当x=0时,y=-6,
当y=0时,x=3,
∴A(3,0),B(0,-6),
∴OA=3,OB=6,
过C作CE⊥x轴于E,
则∠AEC=90°=∠AOB,
∵∠BAC=90°,
∴∠OAB+∠EAC=90°,∠OAB+∠OBA=90°,
∴∠OBA=∠EAC,
∵∠AEC=∠AOB=90°,AB=AC,
∴△OBA≌△EAC,
∴CE=OA=3,AE=OB=6,
∴OE=3+6=9,
∴C(9,-3),
故A点和C点的坐标分别为:A(3,0),C(9,-3).
(2)解:在第四象限内存在一点P,使△PBA≌CAB,
过P作PQ⊥y轴于Q,
∵与(1)中证明△OBA≌△EAC类似证出△PQB≌△BOA,
BQ=OA=3,PQ=OB=6,OQ=6+3=9,
∴P的坐标是(6,-9),
∴在第四象限内存在一点P,使△PBA≌CAB,P的坐标是(6,-9).
(3)解:OQ-DE的值不变,
理由是:过D作DF⊥y轴于F,
∵∠DFQ=∠DQA=90°,
∴∠FDQ+∠FQD=90°,∠FQD+∠FQA=90°,
∴∠FDQ=∠FQA,
∵在△DFQ和△AOQ中
,
∴△DFQ≌△AOQ,
∴FQ=AO=3,
∵∠EOF=∠DFQ=∠DEO=90°,
∴四边形DEOF是矩形,
∴DE=OF,
∴OQ-DE=FQ=3,
即OQ-DE的值不变,OQ-DE=3.
 (1)解:∵
(1)解:∵| k-2 |
| k-3 |
∴k-2=0,
∴k=2,
∴y=2x-6,
当x=0时,y=-6,
当y=0时,x=3,
∴A(3,0),B(0,-6),
∴OA=3,OB=6,
过C作CE⊥x轴于E,
则∠AEC=90°=∠AOB,
∵∠BAC=90°,
∴∠OAB+∠EAC=90°,∠OAB+∠OBA=90°,
∴∠OBA=∠EAC,
∵∠AEC=∠AOB=90°,AB=AC,
∴△OBA≌△EAC,
∴CE=OA=3,AE=OB=6,
∴OE=3+6=9,
∴C(9,-3),
故A点和C点的坐标分别为:A(3,0),C(9,-3).
(2)解:在第四象限内存在一点P,使△PBA≌CAB,
过P作PQ⊥y轴于Q,
∵与(1)中证明△OBA≌△EAC类似证出△PQB≌△BOA,
BQ=OA=3,PQ=OB=6,OQ=6+3=9,
∴P的坐标是(6,-9),
∴在第四象限内存在一点P,使△PBA≌CAB,P的坐标是(6,-9).
(3)解:OQ-DE的值不变,
理由是:过D作DF⊥y轴于F,
∵∠DFQ=∠DQA=90°,
∴∠FDQ+∠FQD=90°,∠FQD+∠FQA=90°,
∴∠FDQ=∠FQA,
∵在△DFQ和△AOQ中
|
∴△DFQ≌△AOQ,
∴FQ=AO=3,
∵∠EOF=∠DFQ=∠DEO=90°,
∴四边形DEOF是矩形,
∴DE=OF,
∴OQ-DE=FQ=3,
即OQ-DE的值不变,OQ-DE=3.
点评:本题考查了全等三角形的性质和判定,三角形的内角和定理,一次函数上点的坐标特征,能综合运用性质进行推理和计算是解此题的关键,题目综合性比较强,有一定的难度.

练习册系列答案
相关题目
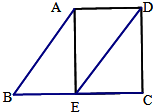
 22、完成下列证明:
22、完成下列证明:

 23、如图,已知AB∥DE,∠BAE=∠EDC,AD⊥AE,垂足为A,请在下划线内补全求∠ADC的度数的解题过程或依据.
23、如图,已知AB∥DE,∠BAE=∠EDC,AD⊥AE,垂足为A,请在下划线内补全求∠ADC的度数的解题过程或依据.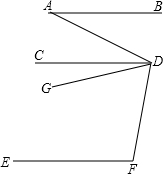
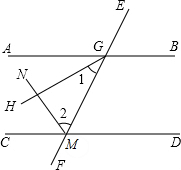 说理填空:如图,已知AB∥CD,GH平分∠AGM,MN平分∠CMG,请说明GH⊥MN的理由.
说理填空:如图,已知AB∥CD,GH平分∠AGM,MN平分∠CMG,请说明GH⊥MN的理由.