题目内容
如下面第一幅图,点A的坐标为(-1,1)(1)那么点B,点C的坐标分别为
(2)若一个关于x,y的二元一次方程,有两个解是
|
|
(3)任取(2)中方程的又一个解(不与前面的解雷同),将该解中x的值作为点D的横坐标,y的值作为点D的纵坐标,在下面第一幅图中描出点D;
(4)在下面第一幅图中作直线AB与直线AC,则直线AB与直线AC的位置关系
是
(5)若把直线AB叫做(2)中方程的图象,类似地请在备用图上画出二元一次方程组
|

分析:(1)由题意,先建立合适的坐标系,再求得点B,点C的坐标;
(2)由(1)写出两个解,再写出这个二元一次方程,并检验点C的坐标是否是这个二元一次方程的解;
(3)先找到点D的坐标,再描出点D;
(4)分别作出直线AB、AC,然后再判断两条直线的位置关系以及点D和直线AB的位置关系;
(5)通过描点、连线作出两个二元一次方程的图象,可发现两条直线的交点坐标恰好是方程组的解.
(2)由(1)写出两个解,再写出这个二元一次方程,并检验点C的坐标是否是这个二元一次方程的解;
(3)先找到点D的坐标,再描出点D;
(4)分别作出直线AB、AC,然后再判断两条直线的位置关系以及点D和直线AB的位置关系;
(5)通过描点、连线作出两个二元一次方程的图象,可发现两条直线的交点坐标恰好是方程组的解.
解答: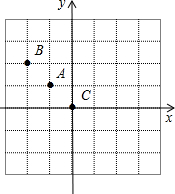 解:(1)∵点A的坐标为(-1,1),∴点B的坐标为(-2,2),点C的坐标为(0,0);
解:(1)∵点A的坐标为(-1,1),∴点B的坐标为(-2,2),点C的坐标为(0,0);
(2)∴
,
,这个二元一次方程为x+y=0,
∵0+0=0,∴点C的坐标值是它的解;
(3)
,点D的坐标为(1,-1),
(4)由(3)题图知,直线AB与直线AC重合,点D在直线AB上;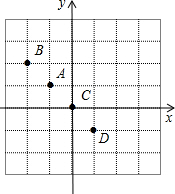
(5)如图:
直线x+y=4与直线x-y=-2的交点为:(1,3);
将x=1,y=3代入原方程组知,
是原方程组的解;
因此二元一次方程组的解,是方程组中两个一次函数图象的交点坐标.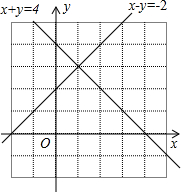
 解:(1)∵点A的坐标为(-1,1),∴点B的坐标为(-2,2),点C的坐标为(0,0);
解:(1)∵点A的坐标为(-1,1),∴点B的坐标为(-2,2),点C的坐标为(0,0);(2)∴
|
|
∵0+0=0,∴点C的坐标值是它的解;
(3)
|
(4)由(3)题图知,直线AB与直线AC重合,点D在直线AB上;

(5)如图:
直线x+y=4与直线x-y=-2的交点为:(1,3);
将x=1,y=3代入原方程组知,
|
因此二元一次方程组的解,是方程组中两个一次函数图象的交点坐标.

点评:此题实际考查的是用图象法解二元一次方程组的方法,比较简单.

练习册系列答案
相关题目