Question

在如图的方格纸中，每个小方格都是边长为1个单位的正方形，△ABC的三个顶点都在格点上（每个小方格的顶点叫格点）．
（1）如果建立直角坐标系，使点B的坐标为（-5，2），点C的坐标为（-2，2），则点A的坐标为

 

；
（2）画出△ABC绕点P顺时针旋转90°后的△A₁B₁C₁，并求线段BC扫过的面积．

Answer 1

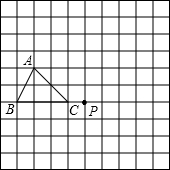
分析：（1）将B点坐标向右平移1个单位，再向上平移2个单位即可得A点的坐标．
（2）连接BP、CP、AP，分别将这三条线段顺时针旋转90°，得到B₁、C₁、A₁，然后顺次连接A₁B₁、B₁C₁、A₁C₁即可得到所求作的△A₁B₁C₁；
线段BC扫过的面积是扇形BPB₁、扇形CPC₁的面积差，由此得解．

解答：解：（1）观察A、B的位置知：将B点向右平移1个单位，再向上平移2个单位，可得A点坐标；故：A（-4，4）．（2分）

（2）如图；（2分）
线段BC扫过的面积=

π

4

（4²-1²）=

15π

4

．（2分）

点评：此题主要考查了旋转变换的作图方法以及扇形面积的计算方法．