题目内容
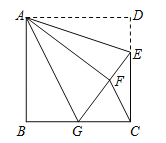
【题目】如图,正方形ABCD的对角线交于点O , 以AD为边向外作Rt△ADE , ∠AED=90°,连接OE , DE=6,OE= ![]() ,则另一直角边AE的长为( ).
,则另一直角边AE的长为( ).
A.![]()
B.2
C.8
D.10
【答案】D
【解析】过点O作OM⊥AE于点M , 作ON⊥DE , 交ED的延长线于点N , ∵∠AED=90°,∴四边形EMON是矩形,∵正方形ABCD的对角线交于点O , ∴∠AOD=90°,OA=OD , ∴∠AOD+∠AED=180°,∴点A , O , D , E共圆,∴∠AEO=∠DEO= ![]() ∠AED=45°,∴OM=ON , ∴四边形EMON是正方形,∴EM=EN=ON , ∴△OEN是等腰直角三角形,∵OE=
∠AED=45°,∴OM=ON , ∴四边形EMON是正方形,∴EM=EN=ON , ∴△OEN是等腰直角三角形,∵OE= ![]() ,∴EN=8,∴EM=EN=8,在Rt△AOM和Rt△DON中
,∴EN=8,∴EM=EN=8,在Rt△AOM和Rt△DON中 ![]() ,∴Rt△AOM≌Rt△DON(HL),∴AM=DN=EN-ED=8-6=2,∴AE=AM+EM=2+8=10.
,∴Rt△AOM≌Rt△DON(HL),∴AM=DN=EN-ED=8-6=2,∴AE=AM+EM=2+8=10.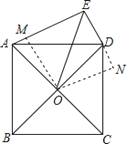
【考点精析】根据题目的已知条件,利用勾股定理的概念的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
相关题目