题目内容
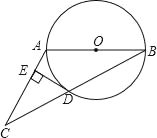
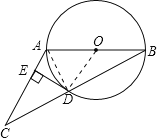
【题目】已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若∠CAB=120°,⊙O的半径等于5,求线段BC的长.
【答案】(1) 见解析;(2)![]()
【解析】试题分析:(1)先连接OD、AD,由于AB是直径以及AB=AC,易证BD=CD,而OA=OB,从而可知OD是△ABC的中位线,那么OD∥AC,再结合DE⊥AC,易证∠ODE=∠CED=90°,即DE是⊙O的切线;
(2)由⊙O半径是5,可知AB=10,而△ABC是等腰三角形,且AD⊥BC,利用等腰三角形三线合一定理可知∠CAD=∠BAD=60°,在Rt△ADB中,易求BD,进而可求BC.
试题解析:如图所示,连接OD、AD.
∵AB是直径,
∴∠BDA=∠CDA=90°,
又∵AB=AC,
∴BD=CD,
∵OA=OB,
∴OD是△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴∠ODE=∠CED=90°,
∴DE是⊙O的切线;
(2)∵⊙O半径是5,
∴AB=10,
∵△ABC是等腰三角形,且AD⊥BC,
∴∠CAD=∠BAD=60°,
在Rt△ADB中,BD=sin60°AB=5![]() ,
,
∴BC=10![]() .
.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
【题目】某水果商店经销一种苹果,共有20筐,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如表:
与标准质量的差值(单位;千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)这20筐苹果中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,这20筐苹果总计超过或不足多少千克?
(3)若苹果每千克售价![]() 元,则出售这20筐苹果可卖多少元?
元,则出售这20筐苹果可卖多少元?