题目内容
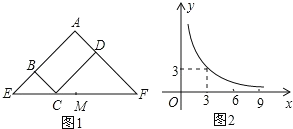
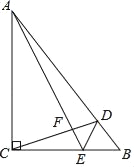
【题目】如图,△ABC,∠ACB=90°,点D,E分别在AB,BC上,AC=AD,∠CDE=45°,CD与AE交于点F,若∠AEC=∠DEB,CE=![]() ,则CF=______.
,则CF=______.
【答案】5
【解析】试题解析延长CE至G,使EC=EG,延长ED至H,使EH=AE,过D作DT∥BC,交AE于T,连接GH、AH,
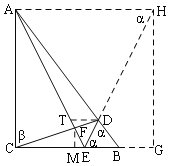
设∠AEC=α,则∠DEB=α,
∵∠AEC=∠DEB=α,
∴△AEC≌△DEB,
∴AC=GH,∠ACE=∠EGH=90°,
∴AC∥GH,
∴四边形ACGH是矩形,
∴AH∥CG,
∴∠AHE=∠HEG=α,
∵AC=AD,
∴∠ACD=∠ADC,
设∠ACD=∠ADC=β,
∵∠CDE=45°,
∴β+45°+∠BDE=180°,
∴β=135°-∠BDE①,
∵△ACD是等腰三角形,
∴∠CAD=180°-2β,
∵△ACB是直角三角形,
∴∠ABC=90°-∠CAD=90°-(180°-2β)=2β-90°,
在△BDE中,由内角和得:α+∠BDE+∠ABC=180°,
α+∠BDE+2β-90°=180°②,
把①代入②得:α+∠BDE+2(135°-∠BDE)-90°=180°,
∠BDE=α,
∴∠ADH=∠BDE=α,
∴AD=AH=AC,
∴四边形ACGH是正方形,
∴AH=AC=2CE=![]() ,
,
∴AD=AC=![]() ,
,
∵∠BED=∠BDE=α,
∴BE=BD,
设BE=x,则BD=x,
在Rt△ACB中,由勾股定理得:AC2+BC2=AB2,
∴(![]() )2+(
)2+(![]() +x)2=(
+x)2=(![]() +x)2,
+x)2,
解得:x=![]() ,
,
∴BE=BD=![]() ,
,
∴CE=2BE=2BD,
∴AD=4BD,
∴![]() ,
,
∵DT∥BC,
∴△ADT∽△ABE,
∴![]() ,
,
∵CE=2BE,
∴![]() ,
,
∵DT∥CE,
∴![]() ,
,
在Rt△ACE中,由勾股定理得:AE=![]()
∴ET=![]() AE=
AE=![]() ×
×![]() =
=![]() ,
,
∴EF=![]() ET=
ET=![]() ×
×![]() =
=![]() ,
,
过F作FM⊥BC于M,
tanα=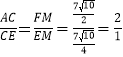 ,
,
设EM=y,则FM=2y,EF=![]() y,
y,
∴![]() y=
y=![]() ,
,
y=![]() ,
,
∴FM=2y=![]() ,EM=y=
,EM=y=![]() ,
,
∴CM=CE-EM=![]() -
-![]() =
=![]() ,
,
在Rt△CFM中,由勾股定理得:CF=![]() =5;
=5;
故答案为:5.