��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У����κ���y=x2+bx+c��ͼ����x�ύ��A��-| 1 | 2 |
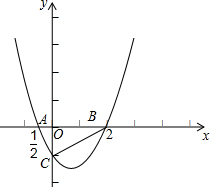 B��2��0��������y�ύ�ڵ�C��
B��2��0��������y�ύ�ڵ�C����1����������ߵĽ���ʽ�����жϡ�ABC����״��
��2����P��x���·�����������һ���㣬����PO��PC�����ѡ�POC��CO���ۣ��õ��ı���POP��C�����ʹ�ı���POP��CΪ���εĵ�P�����ꣻ
��3���ڴ����������Ƿ���ڵ�Q��ʹ����A��C��B��Q�ĵ�Ϊ������ı�����ֱ�����Σ������ڣ����Q������ꣻ�������ڣ�˵�����ɣ�
��������1�����ô���ϵ����������κ����Ľ���ʽ���ɣ������ù��ɶ����涨���ó���ABC����״��
��2���������ε����ʵó�PC=PO���������x2-
x-1=-
���ó�x��ֵ�����ɵó�P������ꣻ
��3���ֱ������BCΪ�ױߣ���BC��AQ���Լ�������ACΪ�ױߣ���BQ��AC���ֱ�������ɵó��𰸣�
��2���������ε����ʵó�PC=PO���������x2-
| 3 |
| 2 |
| 1 |
| 2 |
��3���ֱ������BCΪ�ױߣ���BC��AQ���Լ�������ACΪ�ױߣ���BQ��AC���ֱ�������ɵó��𰸣�
����⣺��1���������⣬��A��-
��0����B��2��0������y=x2+bx+c��
��������ߵĽ���ʽΪy=x2-
x-1��
��x=0ʱ��y=-1�����C������Ϊ��0��-1����
���ڡ�AOC�У�AC=
=
=
��
�ڡ�BOC�У�BC=
=
=
��
AB=OA+OB=
+2=
��
��AC2+BC2=
+5=
=AB2��
���ABC��ֱ�������Σ�
��2����P��������x��x2-
x-1����PP�佻CO��E��
���ı���POP��C�����Σ�
��PC=PO��
����PP����PE��CO��E��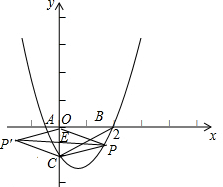
��OE=EC=
��
��y=-
��
��x2-
x-1=-
��
���x1=
��x2=
��
��P���������
��-
����
��-
����
��3�����ڣ��ɣ�1��֪��AC��BC����Q������Ϊ��a��a2-
a-1����
������BCΪ�ױߣ���BC��AQ��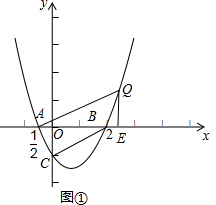
���ABC=��QAB��ͼ��
����Q��QE��x���ڵ�E�����С�QAE�ס�ABC��
��
=
��
=
��
���a1=
��a2=-
����ȥ����
��a=
ʱ��y=
��
���Q��
��
����
������ACΪ�ױߣ���BQ��AC��
���CAB=��QBA��ͼ��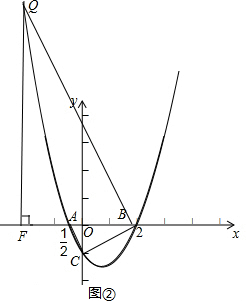
����Q��QF��x���ڵ�F�����С�QBF�ס�BAC��
��
=
��
��
=
��
���a1=-
��a2=2����ȥ����
��a=-
ʱ��y=9��
���Q��-
��9����
����������������Ŀ�����ĵ�QΪ��
��
����-
��9����
| 1 |
| 2 |
��������ߵĽ���ʽΪy=x2-
| 3 |
| 2 |
��x=0ʱ��y=-1�����C������Ϊ��0��-1����
���ڡ�AOC�У�AC=
| OA2+OC2 |
(
|
| ||
| 2 |
�ڡ�BOC�У�BC=
| OB2+OC2 |
| 22+12 |
| 5 |
AB=OA+OB=
| 1 |
| 2 |
| 5 |
| 2 |
��AC2+BC2=
| 5 |
| 4 |
| 25 |
| 4 |
���ABC��ֱ�������Σ�
��2����P��������x��x2-
| 3 |
| 2 |
���ı���POP��C�����Σ�
��PC=PO��
����PP����PE��CO��E��

��OE=EC=
| 1 |
| 2 |
��y=-
| 1 |
| 2 |
��x2-
| 3 |
| 2 |
| 1 |
| 2 |
���x1=
3+
| ||
| 4 |
3-
| ||
| 4 |
��P���������
3+
| ||
| 4 |
| 1 |
| 2 |
3-
| ||
| 4 |
| 1 |
| 2 |
��3�����ڣ��ɣ�1��֪��AC��BC����Q������Ϊ��a��a2-
| 3 |
| 2 |
������BCΪ�ױߣ���BC��AQ��

���ABC=��QAB��ͼ��
����Q��QE��x���ڵ�E�����С�QAE�ס�ABC��
��
| QE |
| AC |
| AE |
| BC |
��
a2-
| ||||
|
a+
| ||
|
���a1=
| 5 |
| 2 |
| 1 |
| 2 |
��a=
| 5 |
| 2 |
| 3 |
| 2 |
���Q��
| 5 |
| 2 |
| 3 |
| 2 |
������ACΪ�ױߣ���BQ��AC��
���CAB=��QBA��ͼ��

����Q��QF��x���ڵ�F�����С�QBF�ס�BAC��
��
| QF |
| BC |
| BF |
| AC |
��
a2-
| ||
|
| 2-a | ||||
|
���a1=-
| 5 |
| 2 |
��a=-
| 5 |
| 2 |
���Q��-
| 5 |
| 2 |
����������������Ŀ�����ĵ�QΪ��
| 5 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
������������Ҫ�����˶��κ������ۺ�Ӧ���Լ����������ε�Ӧ�ã����κ������ۺ�Ӧ���dz��нε��ص������ر�ע���������ν�����ⲿ�ֿ�����ص�Ҳ���ѵ�ͬѧ��Ӧ�ص����գ�

��ϰ��ϵ�д�
 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
�����Ŀ
 ��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD��
��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD�� ��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ�����
��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ����� ��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ
��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ ��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������
��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ��������� ��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��
��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��