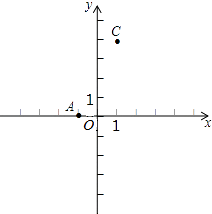Question

【题目】定义：点P是△ABC内部或边上的点（顶点除外），在△PAB，△PBC，△PCA中，若至少有一个三角形与△ABC相似，则称点P是△ABC的自相似点.
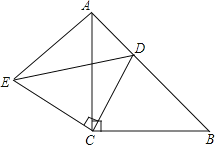
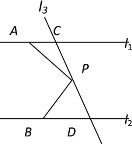
例如：如图1，点P在△ABC的内部，∠PBC=∠A，∠PCB=∠ABC，则△BCP∽△ABC，故点P是△ABC的自相似点.
请你运用所学知识，结合上述材料，解决下列问题：
在平面直角坐标系中，点M是曲线y= （x＞0）上的任意一点，点N是x轴正半轴上的任意一点.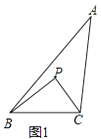

（1）如图2，点P是OM上一点，∠ONP=∠M，试说明点P是△MON的自相似点；当点M的坐标是（ ，3），点N的坐标是（ ，0）时，求点P的坐标；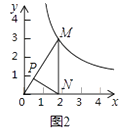

（2）如图3，当点M的坐标是（3， ），点N的坐标是（2，0）时，求△MON的自相似点的坐标；

（3）是否存在点M和点N，使△MON无自相似点？若存在，请直接写出这两点的坐标；若不存在，请说明理由.

Answer 1

【答案】
（1）

解：∵∠ONP=∠M，∠NOP=∠MON，

∴△NOP∽△MON，

∴点P是△MON的自相似点；

过P作PD⊥x轴于D，则tan∠POD= ，

∴∠AON=60°，

∵当点M的坐标是（ ，3），点N的坐标是（ ，0），

∴∠MNO=90°，

∵△NOP∽△MON，

∴∠NPO=∠MNO=90°，

在Rt△OPN中，OP=ONcos60°= ，

∴OD=OPcos60°= × = ，PD=OPsin60°= × = ，

∴P（ ， ）；

（2）

解：作ME⊥x轴于H，如图3所示：

∵点M的坐标是（3， ），点N的坐标是（2，0），

∴OM= =2 ，直线OM的解析式为y= x，ON=2，∠MOH=30°，

分两种情况：

①如图3所示：

∵P是△MON的相似点，

∴△PON∽△NOM，作PQ⊥x轴于Q，

∴PO=PN，OQ= ON=1，

∵P的横坐标为1，

∴y= ×1= ，

∴P（1， ）；

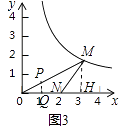
②如图4所示：

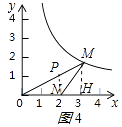
由勾股定理得：MN= =2，

∵P是△MON的相似点，

∴△PNM∽△NOM，

∴ ，即 ，

解得：PN= ，

即P的纵坐标为 ，代入y= 得： = x，

解得：x=2，

∴P（2， ）；

综上所述：△MON的自相似点的坐标为（1， ）或（2， ）；

（3）

解：存在点M和点N，使△MON无自相似点，M（ ，3），N（2 ，0）；理由如下：

∵M（ ，3），N（2 ，0），

∴OM=2 =ON，∠MON=60°，

∴△MON是等边三角形，

∵点P在△ABC的内部，

∴∠PBC≠∠A，∠PCB≠∠ABC，

∴存在点M和点N，使△MON无自相似点.

【解析】（1）由∠ONP=∠M，∠NOP=∠MON，得出△NOP∽△MON，证出点P是△MON的自相似点；过P作PD⊥x轴于D，则tan∠POD= ，求出∠AON=60°，由点M和N的坐标得出∠MNO=90°，由相似三角形的性质得出∠NPO=∠MNO=90°，在Rt△OPN中，由三角函数求出OP= ，OD= ，PD= ，即可得出答案；（2）作ME⊥x轴于H，由勾股定理求出OM=2 ，直线OM的解析式为y= x，ON=2，∠MOH=30°，分两种情况：①作PQ⊥x轴于Q，由相似点的性质得出PO=PN，OQ= ON=1，求出P的纵坐标即可；②求出MN= =2，由相似三角形的性质得出 ，求出PN= ，在求出P的横坐标即可；（3）证出OM=2 =ON，∠MON=60°，得出△MON是等边三角形，由点P在△ABC的内部，得出∠PBC≠∠A，∠PCB≠∠ABC，即可得出结论.
【考点精析】解答此题的关键在于理解反比例函数的图象的相关知识，掌握反比例函数的图像属于双曲线．反比例函数的图象既是轴对称图形又是中心对称图形．有两条对称轴：直线y=x和 y=-x．对称中心是：原点，以及对反比例函数的性质的理解，了解性质:当k＞0时双曲线的两支分别位于第一、第三象限，在每个象限内y值随x值的增大而减小； 当k＜0时双曲线的两支分别位于第二、第四象限，在每个象限内y值随x值的增大而增大．