题目内容
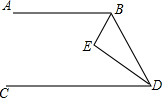如图所示，AB∥CD，BE平分∠ABD，DE平分∠BDC，则∠E是
- A.锐角
- B.直角
- C.钝角
- D.无法确定
B
分析：先利用平行线的性质得到∠ABD+∠BDC=180°，再利用角平分线的性质得到∠E=90°，即是直角．
解答：∵AB∥CD，
∴∠ABD+∠BDC=180°，
又BE平分∠ABD，DE平分∠BDC，
∴∠EBD+∠EDB=90°，
∴∠E=90°，即是直角．
故答案B．
点评：本题重点考查了平行线的性质及角平分线的定义，是一道较为简单的题目．
分析：先利用平行线的性质得到∠ABD+∠BDC=180°，再利用角平分线的性质得到∠E=90°，即是直角．
解答：∵AB∥CD，
∴∠ABD+∠BDC=180°，
又BE平分∠ABD，DE平分∠BDC，
∴∠EBD+∠EDB=90°，
∴∠E=90°，即是直角．
故答案B．
点评：本题重点考查了平行线的性质及角平分线的定义，是一道较为简单的题目．
练习册系列答案
全能练考卷系列答案
一课一练课时达标系列答案
相关题目
5、如图所示，AB∥CD，则∠1+∠2+∠3=（ ）
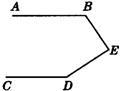24、已知：如图所示，AB∥CD，若∠ABE=130°，∠CDE=152°，则∠BED=
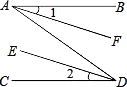如图所示，AB∥CD，需增加什么条件才能使∠1=∠2成立？
如图所示，AB∥CD，EG⊥AB，垂足为G，若∠1=42°，则∠E=