题目内容
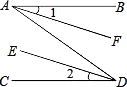 如图所示,AB∥CD,需增加什么条件才能使∠1=∠2成立?
如图所示,AB∥CD,需增加什么条件才能使∠1=∠2成立?分析:此题可以添加条件:①AF∥DE,通过两直线平行,内错角相等,即可证得;②AF,DE分别是∠BAD和∠ADC的平分线,依据也是两直线平行,内错角相等.
解答:解:此题答案不唯一,
条件1:AF∥DE;
理由:∵AB∥CD,AF∥DE,
∴∠BAD=∠CDA,∠FAD=∠EDA,
∴∠BAD-∠FAD=∠CDA-∠EDA,
即∠1=∠2;
条件2:AF,DE分别是∠BAD和∠ADC的平分线;
∵AB∥CD,
∴∠BAD=∠CDA,
∵AF,DE分别是∠BAD和∠ADC的平分线,
∴∠1=
∠BAD,∠2=
∠CDA,
∴∠1=∠2.
条件1:AF∥DE;
理由:∵AB∥CD,AF∥DE,
∴∠BAD=∠CDA,∠FAD=∠EDA,
∴∠BAD-∠FAD=∠CDA-∠EDA,
即∠1=∠2;
条件2:AF,DE分别是∠BAD和∠ADC的平分线;
∵AB∥CD,
∴∠BAD=∠CDA,
∵AF,DE分别是∠BAD和∠ADC的平分线,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1=∠2.
点评:此题考查了平行线的性质:两直线平行,内错角相等.注意此题是开放题,只要符合要求就行.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 5、如图所示,AB∥CD,则∠1+∠2+∠3=( )
5、如图所示,AB∥CD,则∠1+∠2+∠3=( )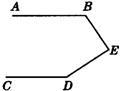 24、已知:如图所示,AB∥CD,若∠ABE=130°,∠CDE=152°,则∠BED=
24、已知:如图所示,AB∥CD,若∠ABE=130°,∠CDE=152°,则∠BED=
 如图所示,AB∥CD,EG⊥AB,垂足为G,若∠1=42°,则∠E=
如图所示,AB∥CD,EG⊥AB,垂足为G,若∠1=42°,则∠E=