Question

【题目】在△ABC，∠BAC为锐角，AB＞AC，AD平分∠BAC交BC于点D．

(1)如图1，若△ABC是等腰直角三角形，直接写出线段AC，CD，AB之间的数量关系；

(2)BC的垂直平分线交AD延长线于点E，交BC于点F．

①如图2，若∠ABE＝60°，判断AC，CE，AB之间有怎样的数量关系并加以证明；

②如图3，若AC+AB＝AE，求∠BAC的度数．

Answer 1

【答案】（1）AB="AC+CD;" （2）①AB=AC+CE，证明见解析;②60°．

【解析】

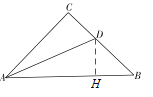
试题（1）如图,过D点作DH⊥AB于点H,则根据角平分线的性质,全等三角形的判定和性质,等腰直角三角形的性质,得AB=AH+HB=AC+DH=AC+CD.

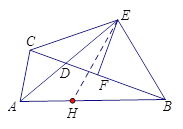
（2）①在线段AB上截取AH=AC，连接EH,证明△EHB是等边三角形即可得出结论.

②在线段AB上截取AH=AC，连接EH，作EM⊥AB于点M,求得得∠EAB=30°,从而∠BAC=2∠EAB=60°．

试题解析：（1）AB=AC+CD.

（2）①AB=AC+CE，证明如下：

如图,在线段AB上截取AH=AC，连接EH．

∵AD平分∠BAC，∴．

又∵AE=AE，∴△ACE≌△AHE．∴CE=HE．

∵EF垂直平分BC，∴CE=BE．

又∠ABE=60°，∴△EHB是等边三角形．

∴BH=HE．∴AB=AH+HB=AC+CE．

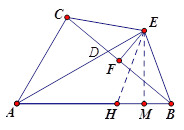
②如图,在线段AB上截取AH=AC，连接EH，作EM⊥AB于点M．

易证△ACE≌△AHE，∴CE=HE．∴△EHB是等腰三角形．∴HM=BM．

∴AC+AB=AH+AB=AM-HM+AM+MB=2AM．

∵，∴．

在Rt△AEM中，，∴∠EAB=30°．

∴∠BAC=2∠EAB=60°．