题目内容
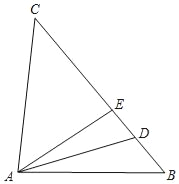
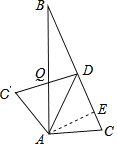
【题目】在Rt△ABC中,∠BAC=90°,AD是△ABC的中线,∠ADC=45°,把△ADC沿AD对折,使点C落在C′的位置,C′D交AB于点Q,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
根据折叠得到对应线段相等,对应角相等,根据直角三角形的斜边中线等于斜边一半,可得出AD=DC=BD,AC=AC′,∠ADC=∠ADC′=45°,CD=C′D,进而求出∠C、∠B的度数,求出其他角的度数,可得AQ=AC,将![]() 转化为
转化为![]() ,再由相似三角形和等腰直角三角形的边角关系得出答案.
,再由相似三角形和等腰直角三角形的边角关系得出答案.
解:如图,过点A作AE⊥BC,垂足为E,
∵∠ADC=45°,
∴△ADE是等腰直角三角形,即AE=DE=![]() AD,
AD,
在Rt△ABC中,
∵∠BAC=90°,AD是△ABC的中线,
∴AD=CD=BD,
由折叠得:AC=AC′,∠ADC=∠ADC′=45°,CD=C′D,
∴∠CDC′=45°+45°=90°,
∴∠DAC=∠DCA=(180°﹣45°)÷2=67.5°=∠C′AD,
∴∠B=90°﹣∠C=∠CAE=22.5°,∠BQD=90°﹣∠B=∠C′QA=67.5°,
∴AC′=AQ=AC,
由△AEC∽△BDQ得:![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() =
=![]() =
=![]() .
.
故选:A.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
【题目】在10盒红色的笔芯中混放了若干支黑色的笔芯,每盒20支笔芯,每盒中混放入的黑色笔芯数如下表:
黑色笔芯数 | 0 | 1 | 4 | 5 | 6 |
盒数 | 2 | 4 | 1 | 2 | 1 |
下列结论:
①黑色笔芯一共有16支;
②从中随机取一盒,盒中红色笔芯数不低于14是必然事件;
③从中随机取一盒,盒中黑色笔芯数不超过4的概率为0.7;
④将10盒笔芯混在一起,从中随机抽取一支笔芯,恰好是黑色的概率是0.12.
其中正确的结论有()
A.1个B.2个C.3个D.4个