题目内容
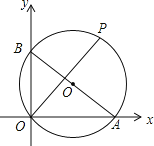
【题目】如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上的一点,且AC平分∠PAE,过C作CD⊥PA于点D.
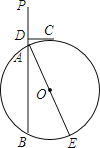
(1)求证:CD为⊙O的切线.
(2)若DC+DA=6,AE=26,求AB的长.
【答案】(1)见解析;(2)AB=24.
【解析】
试题分析:(1)连接OC,根据OA=OC推出∠OCA=∠OAC,根据角平分线得出∠OCA=∠OAC=∠CAP,推出OC∥AP,得出OC⊥CD,根据切线的判定推出即可;
(2)过O作OM⊥AB于M,得出矩形OMDC,推出OM=CD,OC=AM+AD,求出AM=13﹣DA,利用勾股定理求出AD的长,即可求出AM的长,从而求出AB的长.
(1)证明:连接OC.
∵OC=OA,
∴∠OAC=∠OCA.
∵AC平分∠PAE,
∴∠DAC=∠OAC,
∴∠DAC=∠OCA,
∴AD∥OC.
∵CD⊥PA,
∴∠ADC=∠OCD=90°,
即 CD⊥OC,点C在⊙O上,
∴CD是⊙O的切线.
(2)解:过O作OM⊥AB于M.即∠OMA=90°,AM=BM,
∵∠MDC=∠OMA=∠DCO=90°,
∴四边形DMOC是矩形,
∴OC=DM,OM=CD.
∵AE=26,
∴AO=13,
∴OC=AO=13,
∴DM=13,
∴AM=13﹣DA,
∵DC+DA=6,
∴OM=CD=6﹣DA,
∵在Rt△AMO中,∠AMO=90°,根据勾股定理得:AO2=AM2+OM2.
∴132=(6﹣DA)2+(13﹣DA)2,
∴DA=1或DA=18(舍去),
∴AM=13﹣1=12,
∴AB=2AM=24.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目