Question

【题目】阅读材料，解答问题

数学课上，同学们兴致勃勃地探讨着利用不同画图工具画角的平分线的方法．

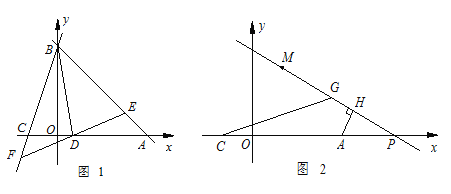
小惠说：“如图1，我用相同的两块含 30°角的直角三角板可以画角的平分线．画法如下：

①在 的两边分别取点 M，N，使 OM=ON ；

②把直角三角板按如图所示的位置放置，两斜边交于点 P ；

③作射线 OP .则OP是∠AOB 的平分线．”小旭说：“我只用刻度尺就可以画角平分线．”

请你也参与探讨，解决以下问题：

（1）小惠的作法正确吗?若正确，请给出证明，若不正确，请说明理由．

（2）请你和小旭一样，只用刻度尺画出图 2 中∠QRS 的平分线，并简述画图的过程．

Answer 1

【答案】(1) 小惠的作法正确．理由见解析；（2）见解析

【解析】试题分析：（1）过O点作OC⊥PM于C，OD⊥PN于D，求出△OMC≌△OND，根据全等三角形的性质得出OC=OD，∠COM=∠DON，根据角平分线性质求出∠CPO=∠DPO．根据三角形内角和定理求出即可；

（2）根据全等三角形的判定定理SSS，用刻度尺作出即可．

试题解析：解：（1）小惠的做法正确．

理由如下：

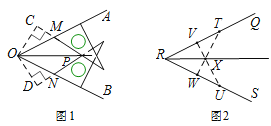
如图1，过O点作OC⊥PM于C，OD⊥PN于D，∴∠C=∠D=90°，由题意，∠PMA=∠PNB=60°，∴∠OMC=∠PMA=60°，∠OND=∠PNB=60°，∴∠OMC=∠OND．

在△OMC和△OND中，∵∠CMO=∠DNO，∠C=∠D，OM=ON，∴△OMC≌△OND（AAS），∴OC=OD，∠COM=∠DON，∵OC⊥PM于C，OD⊥PN于D，∴点O在∠CPD的平分线上，∴∠CPO=∠DPO，∴∠COP=∠DOP，∴∠MOP=∠NOP，即 射线OP是∠AOB的平分线；

（2）如图2，射线RX是∠QRS的平分线，作图过程是：用刻度尺作RV=RW，RT=RU，连接TW，UV交于点X，射线RX即为所求∠QRS的平分线．