Question

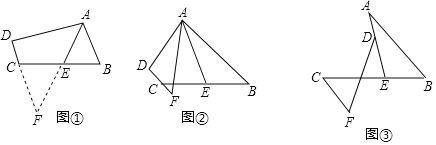
【题目】如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，求∠A，∠ADB的度数。

Answer 1

【答案】∠A=36°,∠ADB=108°

【解析】试题分析：根据等边对等角可得∠ABC=∠C，∠A=∠ABD，∠C=∠BDC，再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BDC=∠A+∠ABD=2∠A，然后根据三角形的内角和定理列出方程求解即可．

试题解析：

∵AB=AC，

∴∠ABC=∠C，

∵BD=BC=AD，

∴∠A=∠ABD，∠C=∠BDC，

在△ABD中，∠BDC=∠A+∠ABD=2∠A，

在△ABC中，∠A+∠ABC+∠C=180°，

∴∠A+2∠A+2∠A=180°，

解得∠A=36°，

∴∠ADB=180°-∠A-∠ABD=180°-36°-36°=108°．