题目内容
 如图,D在AB上,E在AC上,且∠B=∠C,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是
如图,D在AB上,E在AC上,且∠B=∠C,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是
- A.AD=AE
- B.∠AEB=∠ADC
- C.BE=CD
- D.AB=AC
B
分析:根据AAS即可判断A;根据三角对应相等的两三角形不一定全等即可判断B;根据AAS即可判断C;根据ASA即可判断D.
解答:A、根据AAS(∠A=∠A,∠C=∠B,AD=AE)能推出△ABE≌△ACD,正确,故本选项错误;
B、三角对应相等的两三角形不一定全等,错误,故本选项正确;
C、根据AAS(∠A=∠A,∠B=∠C,BE=CD)能推出△ABE≌△ACD,正确,故本选项错误;
D、根据ASA(∠A=∠A,AB=AC,∠B=∠C)能推出△ABE≌△ACD,正确,故本选项错误;
故选B.
点评:本题考查了对全等三角形的判定的应用,注意:全等三角形的判定方法只有SAS,ASA,AAS,SSS,共4种,主要培养学生的辨析能力.
分析:根据AAS即可判断A;根据三角对应相等的两三角形不一定全等即可判断B;根据AAS即可判断C;根据ASA即可判断D.
解答:A、根据AAS(∠A=∠A,∠C=∠B,AD=AE)能推出△ABE≌△ACD,正确,故本选项错误;
B、三角对应相等的两三角形不一定全等,错误,故本选项正确;
C、根据AAS(∠A=∠A,∠B=∠C,BE=CD)能推出△ABE≌△ACD,正确,故本选项错误;
D、根据ASA(∠A=∠A,AB=AC,∠B=∠C)能推出△ABE≌△ACD,正确,故本选项错误;
故选B.
点评:本题考查了对全等三角形的判定的应用,注意:全等三角形的判定方法只有SAS,ASA,AAS,SSS,共4种,主要培养学生的辨析能力.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 15、如图,D在AB上,E在AC上,且∠B=∠C,请添加一个条件,使△ABE≌△ACD,你添加的条件是
15、如图,D在AB上,E在AC上,且∠B=∠C,请添加一个条件,使△ABE≌△ACD,你添加的条件是
 5、如图,D在AB上,E在AC上,且∠B=∠C,则下列条件中,无法判定△ABE≌△ACD的是( )
5、如图,D在AB上,E在AC上,且∠B=∠C,则下列条件中,无法判定△ABE≌△ACD的是( )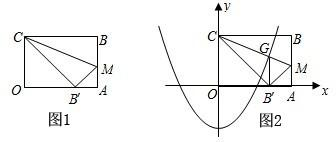 这条抛物线所对应的函数关系式.
这条抛物线所对应的函数关系式.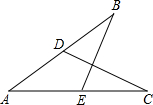 如图,D在AB上,E在AC上,且∠B=∠C,那么补充下列一个条件
如图,D在AB上,E在AC上,且∠B=∠C,那么补充下列一个条件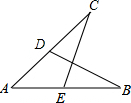 如图,E在AB上,D在AC上,且∠B=∠C,那么补充下列一个条件后,仍无法判定△ABD≌△ACE的是( )
如图,E在AB上,D在AC上,且∠B=∠C,那么补充下列一个条件后,仍无法判定△ABD≌△ACE的是( )