题目内容
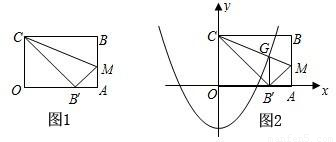
已知OABC是一张矩形纸片,AB=6.(1)如图1,在AB上取一点M,使得△CBM与△CB′M关于CM所在直线对称,点B′恰好在边OA上,且△OB′C的面积为24cm2,求BC的长;
(2)如图2.以O为原点,OA、OC所在直线分别为x轴、y轴建立平面直角坐标系.求对称轴CM所在直线的函数关系式;
(3)作B′G∥AB交CM于点G,若抛物线y=
| 1 | 6 |
 这条抛物线所对应的函数关系式.
这条抛物线所对应的函数关系式.
分析:(1)S△OB′C=
OC•OB′=24,可得OB′=8,在三角形OCB′中,根据勾股定理知B′C=BC=10;
(2)由(1)知,C点坐标为(0,6),B′A=OA-OB′=10-8=2,设AM=x,则BM=B'M=6-x,则在Rt△AB′M中,根据勾股定理可列方程,从而求出AM,即可得M点坐标,然后根据待定系数法求出直线CM的解析式.
(3)由(1)知,B点坐标为(8,0),又B′G∥AB,所以G点横坐标为8,因为G也在直线CM上,由(2)可得G点纵坐标,然后把G点坐标代入y=
x2+m中,求出m,即可解答.
| 1 |
| 2 |
(2)由(1)知,C点坐标为(0,6),B′A=OA-OB′=10-8=2,设AM=x,则BM=B'M=6-x,则在Rt△AB′M中,根据勾股定理可列方程,从而求出AM,即可得M点坐标,然后根据待定系数法求出直线CM的解析式.
(3)由(1)知,B点坐标为(8,0),又B′G∥AB,所以G点横坐标为8,因为G也在直线CM上,由(2)可得G点纵坐标,然后把G点坐标代入y=
| 1 |
| 6 |
解答:解:(1)如图1,∵△OB′C的面积为24cm2,且OC=AB=6cm.
∴OB′=2×24÷6=8cm
∴B′C=
=10cm
∴BC=B′C=10cm.
(2)由(1)可知B′A=OA-OB′=10-8=2
设AM=x,则BM=B′M=6-x
由勾股定理可得方程:22+x2=(6-x)2
解得:x=
所以M(10,
),C(0,6)
设CM所在直线的函数关系式为y=kx+b
则
,
解得
,
∴CM所在直线的函数关系式为y=-
x+6.
(3)∵B′G∥AB,OB′=8
∴G点的横坐标为8,
又∵点G在直线CM上,CM关系式为y=-
x+6
所以G点的纵坐标为y=-
×8+6=
即G(8,
).
∵抛物线y=
x2+m过点G,
∴
=
×82+m
∴m=-
所求抛物线的关系式为y=
x2-
.
∴OB′=2×24÷6=8cm
∴B′C=
| 62+82 |
∴BC=B′C=10cm.
(2)由(1)可知B′A=OA-OB′=10-8=2
设AM=x,则BM=B′M=6-x
由勾股定理可得方程:22+x2=(6-x)2
解得:x=
| 8 |
| 3 |
所以M(10,
| 8 |
| 3 |
设CM所在直线的函数关系式为y=kx+b
则
|
解得
|
∴CM所在直线的函数关系式为y=-
| 1 |
| 3 |
(3)∵B′G∥AB,OB′=8
∴G点的横坐标为8,
又∵点G在直线CM上,CM关系式为y=-
| 1 |
| 3 |
所以G点的纵坐标为y=-
| 1 |
| 3 |
| 10 |
| 3 |
即G(8,
| 10 |
| 3 |
∵抛物线y=
| 1 |
| 6 |
∴
| 10 |
| 3 |
| 1 |
| 6 |
∴m=-
| 22 |
| 3 |
所求抛物线的关系式为y=
| 1 |
| 6 |
| 22 |
| 3 |
点评:此题主要考查了勾股定理、待定系数法,难易程度适中.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 x2+m过点G,求这条抛物线所对应的函数关系式.
x2+m过点G,求这条抛物线所对应的函数关系式.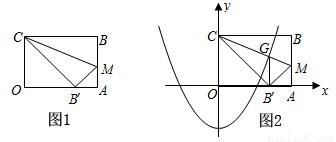
 x2+m过点G,求这条抛物线所对应的函数关系式.
x2+m过点G,求这条抛物线所对应的函数关系式.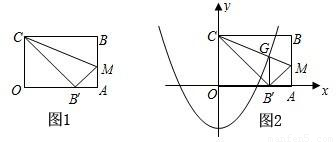
 x2+m过点G,求这条抛物线所对应的函数关系式.
x2+m过点G,求这条抛物线所对应的函数关系式.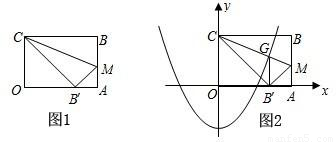
 x2+m过点G,求这条抛物线所对应的函数关系式.
x2+m过点G,求这条抛物线所对应的函数关系式.