题目内容
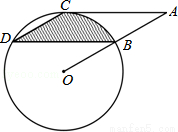
(2013年四川自贡12分)在东西方向的海岸线l上有一长为1km的码头MN(如图),在码头西端M的正西19.5km处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距 km的C处.
km的C处.

(1)求该轮船航行的速度(保留精确结果);
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.
【答案】
解:(1)如图,∵∠1=30°,∠2=60°,∴△ABC为直角三角形。
∵AB=40km,AC=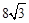 km,
km,
∴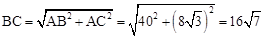 (km)。
(km)。
∵1小时20分钟=80分钟,1小时=60分,
∴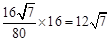 (千米/小时)。
(千米/小时)。
答:该轮船航行的速度为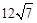 千米/小时。
千米/小时。
(2)作线段BR⊥x轴于R,作线段CS⊥x轴于S,延长BC交l于T。

∵∠2=60°,∴∠4=90°﹣60°=30°。
∵AC=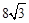 km,∴CS=
km,∴CS=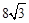 sin30°=
sin30°=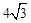 (km),AS=
(km),AS=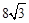 cos30°=
cos30°=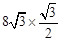 =12(km)。
=12(km)。
又∵∠1=30°,∴∠3=90°﹣30°=60°。
∵AB=40km,∴BR=40•sin60°=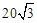 (km),AR=40×cos60°=40×
(km),AR=40×cos60°=40×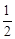 =20(km)。
=20(km)。
易得,△STC∽△RTB,∴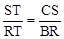 ,即
,即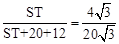 ,解得:ST=8(km)。
,解得:ST=8(km)。
∴AT=12+8=20(km)。
又∵AM=19.5km,MN长为1km,∴AN=20.5km。
∵19.5<AT<20.5,∴轮船能够正好行至码头MN靠岸。
【解析】(1)根据∠1=30°,∠2=60°,可知△ABC为直角三角形.根据勾股定理解答。
(2)延长BC交l于T,比较AT与AM、AN的大小即可得出结论。
考点:解直角三角形的应用(方向角问题),锐角三角函数定义,特殊角的三角函数值,勾股定理,相似三角形的判定和性质。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
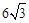 cm.
cm.