Question

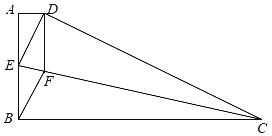
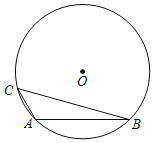
【题目】已知，把45°的直三角板的直角顶点E放在边长为6的正方形ABCD的一边BC上，直三角板的一条直角边经过点D，以DE为一边作矩形DEFG，且GF过点A，得到图1．

（1）求矩形DEFG的面积；

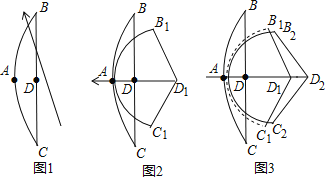
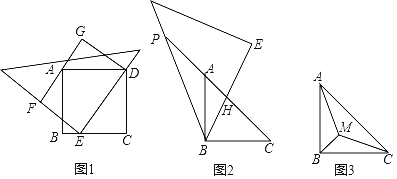
（2）若把正方形ABCD沿着对角线AC剪掉一半得到等腰直角三角形ABC，把45°的直三角板的一个45°角的顶点与等腰直角三角形ABC的直角顶点B重合，直三角板夹这个45°角的两边分别交CA和CA的延长线于点H、P，得到图2．猜想：CH、PA、HP之间的数量关系，并说明理由；

（3）若把边长为6的正方形ABCD沿着对角线AC剪掉一半得到等腰直角三角形ABC，点M是Rt△ABC内一个动点，连接MA、MB、MC，设MA+MB+MC＝y，直接写出 的最小值．

Answer 1

【答案】（1）36；（2）CH2+PA2＝HP2，理由见解析；（3）72+36．

【解析】

（1）根据正方形的性质得到∠ADC＝∠DCE＝90°，根据矩形的性质得到∠AGD＝∠GDE＝90°，根据相似三角形的性质和矩形的面积公式即可得到结论；

（2）根据旋转的性质得到BK＝BP，∠PBA＝∠KBC，∠BCK＝∠BAP＝ ＝135°，由勾股定理得到，求得∠PBA+∠ABE＝45°，通过等量代换得到∠KBC+∠ABE＝45°，根再据全等三角形的性质得到HK＝HP，根据勾股定理即可得到结论；

（3）根据旋转的性质得到MC＝KN，BM＝BK，根据等边三角形的性质得到MK＝BM，于是得到MA+MB+MC＝AM+MK+KN，当A，M，K，N四点共线时，AN就是所求的MA+MB+MC的最小值，过N作NQ⊥AB交AB的延长线于Q，求得AQ＝AB+BQ＝，再根据勾股定理即可得到结论．

解：（1）∵四边形ABCD是正方形，

∴∠ADC＝∠DCE＝90°，

∵四边形DEFG是矩形，

∴∠AGD＝∠GDE＝90°，

∴∠DCE＝∠AGD＝90°，∠ADC＝∠GDE＝90°，

∴∠ADC﹣∠ADE＝∠GDE﹣∠ADE，

∴∠EDC＝∠ADG，

∵∠EDC＝∠ADG，∠DCE＝∠AGD＝90°，

∴△ECD∽△AGD，

∴，

∴DGDE＝DCDA＝6×6＝36，

∴矩形DEFG的面积＝DGDE＝36；

（2），

证明：把△BAP绕着点B顺时针旋转90°得到△BCK，连接KH，

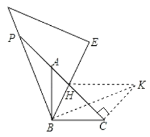
由旋转得△BAP≌△BCK，

∴BK＝BP，∠PBA＝∠KBC，∠BCK＝∠BAP＝，

∴∠HCK＝＝，

∴由勾股定理得，，

∵∠PBE＝45°，

∴∠PBA+∠ABE＝45°，

∵∠PBA＝∠KBC，

∴∠KBC+∠ABE＝45°，

∵∠ABC＝90°，

∴∠HBK＝45°，

∵∠PBE＝45°，

∴∠HBK＝∠PBE＝45°，

∵BK＝BP，∠HBK＝∠PBE，BH＝BH，

∴△BHP≌△BHK（SAS），

∴HK＝HP，

∵，

∴；

（3）把△BMC绕着点B顺时针旋转60°得到△BKN，连接MK，BN，NC，

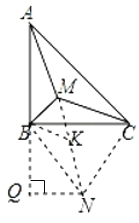
由旋转得，△BMC≌△BKN，

∴MC＝KN，BM＝BK，

∵BM＝BK，∠MBK＝60°，

∴△BKM是等边三角形，

∴MK＝BM，

∴MA+MB+MC＝AM+MK+KN，

当A，M，K，N四点共线时，AN就是所求的MA+MB+MC的最小值，

过N作NQ⊥AB交AB的延长线于Q，

∵，∠BQN＝90°，

∴QN＝BNsin30°＝6×＝3，BQ＝BNcos30°＝，

∴AQ＝AB+BQ＝ ，

在Rt△AQN中，由勾股定理得， ，

∴的最小值为．