��Ŀ����
����Ŀ����֪ʶ���ɣ�����֪���������ֲ�ͬ�ķ�������ͬһ������ͼ�ε���������Եõ�һЩ�������ʽ.
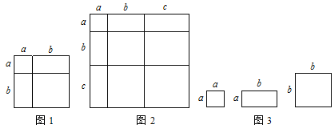
���磺��ͼ���Եõ�(a+b)2=a2+2ab+b2�����ڴˣ������������⣺
�� ������ͼ��д��һ���������ʽ��
![]() ��
��
�� ���â��еõ��Ľ��ۣ������������⣺��a+b+c=12��![]() ��
��
��![]() ��
��
�� С��ͬѧ����ͼ��x�ű߳�Ϊa�������Σ�y�ű߳�Ϊb�������Σ�z�ſ������ֱ�Ϊa��b�ij�����ֽƬƴ��һ�����Ϊ(2a+b)(a+3b)�ij����Σ���x��y��z= ��
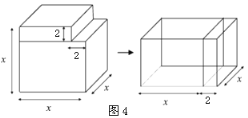
��֪ʶǨ�ƣ��� ���Ƶأ������ֲ�ͬ�ķ������㼸��������ͬ�����Եõ�һЩ�������ʽ����ͼ��ʾ����һ���߳�Ϊx����������ȥһ���߳�Ϊ2��С�����������ƴ��һ���³����壮���������ͼ������ͼ�εı仯��ϵ��д��һ���������ʽ��
���𰸡���(a+b+c)2=a2+b2+c2+2ab+2ac+2bc�� �� 90�� �� 12�� �� x3-4x=x(x-2)(x-2)��
��������
��1�����������ε����=��a+b+c��2�������ε����=a2+b2+c2+2ab+2ac+2bc���ɵõ�ʽ��
��2������a2+b2+c2=��a+b+c��2-2ab-2ac-2bc�����м��㼴�ɣ�
��3��������ƴͼ�ε����Ϊ��xa2+yb2+zab����(2a+b)(a+3b)= 2a2+6ab+3b2�����ɵõ�x��y��z��ֵ��
��4������ԭ����������=�¼�������������ʽ�ɵý��ۣ�
��1����ͼ2�ã������ε����=��a+b+c��2�������ε����=a2+b2+c2+2ab+2ac+2bc��
�ࣨa+b+c��2=a2+b2+c2+2ab+2ac+2bc��
�ʴ�Ϊ����a+b+c��2=a2+b2+c2+2ab+2ac+2bc��
��2���ߣ�a+b+c��2=a2+b2+c2+2ab+2ac+2bc��
��a+b+c=12��ab+ac+bc=27��
��122=a2+b2+c2+2��27��
��a2+b2+c2=144-54=90��
�ʴ�Ϊ��90��
��3��������ã�(2a+b)(a+3b)=xa2+yb2+zab��
��2a2+7ab+3b2=xa2+yb2+zab��
![]() ,
,
��x+y+z=12��
�ʴ�Ϊ��12��
��4����ԭ����������=x3-2��2x=x3-4x���¼���������=��x+2����x-2��x��
��x3-4x=��x+2����x-2��x��
�ʴ�Ϊ��x3-x=��x+2����x-2��x��