题目内容
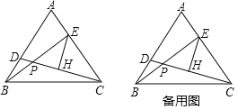
【题目】如图,在等边△ABC中,点D、点E分别在AB、AC上,BD=AE,连接BE、CD交于点P,作EH⊥CD于H.
(1)求证:△CAD≌△BCE;(2)求证:PE=2PH;(3)若PB=PH,求∠ACD的度数.
【答案】(1)详见解析;(2)详见解析;(3)45°
【解析】
(1)根据SAS证明△CAD≌△BCE即可;
(2)利用直角三角形30度角的性质即可解决问题;
(3)连接AH、BH,过H点作HM⊥AB于M,HN⊥AC于N.利用全等三角形的性质证明△EHC是等腰直角三角形即可解决问题;
(1)证明:如图1中,

∵△ACB是等边三角形,
∴∠A=∠BCA=∠ABC=60°,AB=AC=BC,
∵BD=AE,
∴AB-BD=AC-AE,
即AD=EC,
在△CAD与△BCE中,
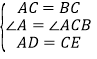 ,
,
∴△CAD≌△BCE(SAS).
(2)证明:如图2中,
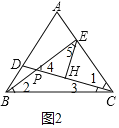
由(1)得△CAD≌△BCE,
∴∠1=∠2,
∵∠1+∠3=60°,
∴∠2+∠3=60°,
∴∠4=∠2+∠3=60°,
又∵EH⊥CD,
∴∠PHE=90°即△PHE是直角三角形,
∵∠5=90°-∠4=30°,
∴PH=![]() PE.
PE.
即PE=2PH.
(3)解:连接AH、BH,过H点作HM⊥AB于M,HN⊥AC于N.
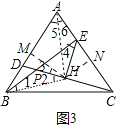
∵PB=PH,
∠1=∠2,
由(2)得,∠4=30°,
∠3=∠1+∠2=60°,
∴∠1=∠2=30°,
∴∠BHE=120°,
∴∠1=∠4,
∴BH=EH,
∵∠BAC=60°,
∴∠ABH+∠AEH=360°-∠BAC+∠BHE=180°,
∵∠HEC+∠AEH=180°,
∠ABH=∠HEC,
∴∠BMH=∠ENH=90°,
∴△BHM≌△EHN(AAS),
∴HM=HN,
∴∠5=∠6,
∵AH=AH,AB=AC,
∴△AHB≌△AHC(SAS0,
∴HB=HC=HE且∠EHC=90°.
∴∠ACD=45°.