Question

【题目】如图，已知反比例函数y=(k≠0)的图象与一次函数y=k'x+b(k'≠0)的图象相交于A和B两点。

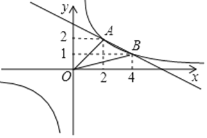
(1)求反比例函数和一次函数的表达式；

(2)观察两函数在同一坐标系中的图象，直接写出关于x的不等式<k'x+b的解集；

(3)求△AOB的面积.(其中O为坐标原点)

Answer 1

【答案】(1)反比例函数表达式为y=；一次函数表达式为y=；(2)x＜0或2＜x＜4；(3)3

【解析】

（1）运用待定系数法，根据A和B两点坐标即可得到反比例函数和一次函数的表达式；

（2）由函数图象的上下位置关系可得，不等式＜k′x+b的解集为x＜0或2＜x＜4；

（3）先求得直线AB与x轴的交点坐标，即可得到△AOB的面积．

（1）把A（2，2）代入反比例函数y=（k≠0），可得，

k=2×2=4，

∴反比例函数的表达式为y=；

把A（2，2），B（4，1）代入一次函数y=k′x+b（k′≠0），可得

，

解得，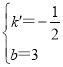

∴一次函数的表达式为y=-x+3；

（2）由图可得，不等式＜k′x+b的解集为x＜0或2＜x＜4．

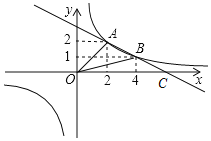
（3）在y=-x+3中，令y=0，则0=-x+3，

解得x=6，

∴C（6，0），

∴S△AOB=S△AOC-S△BOC

=×6×2-×6×1

=6-3

=3．