Question

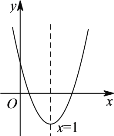
【题目】如图，顶点为M的抛物线y=a(x+1)2-4分别与x轴相交于点A，B(点A在点B的)右侧)，与y轴相交于点C(0，﹣3)．

(1)求抛物线的函数表达式；

(2)判断△BCM是否为直角三角形，并说明理由．

(3)抛物线上是否存在点N(不与点C重合)，使得以点A，B，N为顶点的三角形的面积与S△ABC的面积相等？若存在，求出点N的坐标；若不存在，请说明理由．

Answer 1

【答案】(1)；(2)见解析；(3)存在，(，3)，(，3)，(，)

【解析】

(1)用待定系数法求出抛物线解析式即可；
(2)由抛物线解析式确定出抛物线的顶点坐标和与x轴的交点坐标，用勾股定理的逆定理即可；
(3)根据题意得出，然后求出，再代入求解即可．

(1)∵抛物线与轴相交于点C(0，-3)．
∴，
∴，
∴抛物线解析式为，
(2)△BCM是直角三角形，
理由：由(1)有，抛物线解析式为，
∴顶点为M的坐标为(-1，-4)，
由(1)抛物线解析式为，
令，，
∴，
∴点A的坐标为(1，0)，点B的坐标为(-3，0)，
∴，

，

=，

∵，

∴，
∴△BCM是直角三角形，

(3)设N点纵坐标为，

根据题意得，即，

∴，

当N点纵坐标为3时，，

解得：

当N点纵坐标为-3时，，

解得：(与点C重合，舍去)，

∴N点坐标为(，3)，(，3)，(，)，