题目内容
【题目】在平面直角坐标系xOy中,已知点A(0,2),直线OP位于一、三象限,∠AOP=45°(如图1),设点A关于直线OP的对称点为B.
(1)写出点B的坐标;
(2)过原点O的直线l从OP的位置开始,绕原点O顺时针旋转. ①如图1,当直线l顺时针旋转10°到l1的位置时,点A关于直线l1的对称点为C,则∠BOC的度数是 , 线段OC的长为;
②如图2,当直线l顺时针旋转55°到l2的位置时,点A关于直线l2的对称点为D,则∠BOD的度数是;
③直线l顺时针旋转n°(0<n≤90),在这个运动过程中,点A关于直线l的对称点所经过的路径长为(用含n的代数式表示).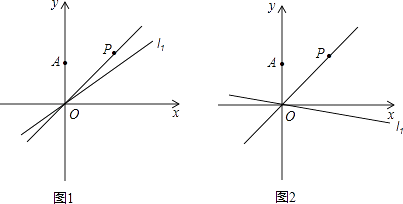
【答案】
(1)解:如图
A关于直线OP的对称点正好落在x轴上,
∵根据轴对称性质∴得出OA=OB=2,
∴B点的坐标是(2,0)

(2)20°;2;110°;![]()
【解析】(2)解: 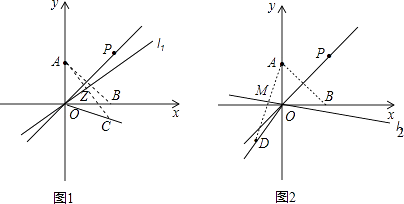 ①如图1,过A作AZ⊥直线l1于Z,延长AZ到C,使AZ=ZC,则C为A关于直线l1的对称点,
①如图1,过A作AZ⊥直线l1于Z,延长AZ到C,使AZ=ZC,则C为A关于直线l1的对称点,
∵根据轴对称性质得出OA=OC=2,
∴∠AOZ=∠COZ=45°+10°=55°,
∴∠BOC=55°+55°﹣90°=20°,
所以答案是:20°,2;
②解:如图2,过A作AM⊥直线l2于M,延长AM到D,使AM=MD,则D为A关于直线l2的对称点,
∵根据轴对称性质得出OA=OD,
∴∠AOM=∠DOM=180°﹣(45°+55°)=80°,
80°+80°﹣90°=70°,
∴∠BOD=180°﹣70°=110°,
所以答案是:110°;
③解:直线l顺时针旋转n°(0<n≤90),在这个运动过程中,点A关于直线l的对称点所经过的路径为以O为圆心,以2为半径的弧BQ(Q为A关于旋转n°后直线l1的对称点),
圆心角∠BOQ=2(45°+n°)﹣90°=2n°,
由弧长公式得: ![]() =
= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】利用弧长计算公式和旋转的性质对题目进行判断即可得到答案,需要熟知若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
餐桌 | a | 270 | 500元 |
餐椅 | a﹣110 | 70 |
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
(3)由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,按照(2)中获得最大利润的方案购进餐桌和餐椅,在调整成套销售量而不改变销售价格的情况下,实际全部售出后,所得利润比(2)中的最大利润少了2250元.请问本次成套的销售量为多少?






