Question

【题目】如图，是的直径，若，，以为边作圆的内接正多边形，则这个正多边形是________边形．

Answer 1

【答案】6

【解析】

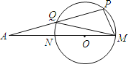
首先根据圆周角定理得出∠POQ＝80°，进而利用等腰三角形的性质得出∠OPQ＝∠OQP，再由外角的性质得出∠A＋∠APO＝∠POM＝60°，即可得出△POM是等边三角形，再由正六边形的性质得出答案.

如图，连接QO，PO，∵QO=PO，∴∠OPQ=∠OQP，∵∠PMQ=40°，∴∠POQ=80°，
∴∠OPQ+∠OQP=180°80°=100°，∴∠OPQ=∠OQP=50°，∴∠A+∠APO=∠POM=10°+50°=60°，∵PO=OM，∴△POM是等边三角形，∴PM=OP=OM，∴以PM为边作圆的内接正多边形，则这个正多边形是正六边形.故答案为6.