题目内容
【题目】数学活动课上,老师出示了一个问题:
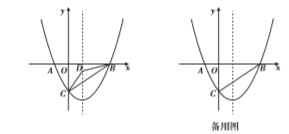
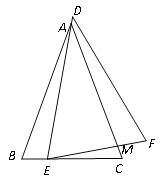
如图,△ABC≌△DEF(点A、B分别与点D、E对应),AB=AC.现将△ABC与△DEF按如图所示的方式叠放在一起,现将△ABC保持不动, △DEF运动,且满足点E在BC边从B向C移动(不与B、C重合),DE始终经过点A,EF与AC边交于点M.求证:△ABE∽△ECM.
(1)请解答老师提出的问题.
(2)受此问题的启发,小明将△DEF绕点E按逆时针旋转, DE、EF分别交线段AB、AC边于点N、M,连接MN,如图2,当EB=EC时,小明猜想△NEM与△ECM相似.小明的猜想正确吗?请你作出判断,并说明理由.
(3)在(2)的条件下,以E为圆心,作⊙E,使得AB与⊙E相切,请在图3中画出⊙E,并判断直线MN与⊙E的位置关系,说明理由.
【答案】(1)证明见解析;(2)小明是猜想是正确的,即△NEM∽△ECM;(3)直线MN与⊙E的位置关系是相切.
【解析】
(1)证明:由如图1,△ABC≌△DEF(点A、B分别与点D、E对应),AB=AC,
得∠ABE=∠ECM,又∠AEC=∠ABE+∠BAE=∠AEC+∠CEM,
所以∠BAE=∠CEM,所以△ABE∽△ECM.
(2)小明是猜想是正确的,即△NEM∽△ECM
理由如下:同(1)可证得,△NBE∽△ECM,所以![]() ∠BNE=∠CEM,
∠BNE=∠CEM,
又BE=CE,所以![]()
又∠C=∠NEM
所以△NEM∽△ECM
(3)直线MN与⊙E的位置关系是相切.
理由如下:由(2)知,∠BNE=∠CEM,∠ENM=∠CEM,
所以∠BNE=∠ENM.
过E点做EH⊥MN于H,⊙E 与AB切于G点,由于E点在∠BNM 的平分线上,EH=GE,所以点H在⊙E上,所以MN是⊙E的切线,直线MN与⊙E的位置关系是相切.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
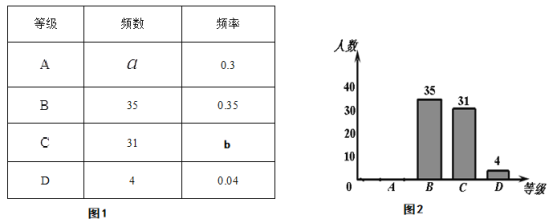
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
(1)这天部分出行学生使用共享单车次数的中位数是 ,众数是 .
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少名.