Question

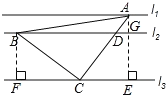
【题目】如图，直线l1∥l2∥l3，一等腰直角三角形ABC的三个顶点A、B、C分别在l1、l2、l3上，AC交l2于D，∠ACB=90°．已知l1与l2的距离为2，l2与l3的距离为6，则的值为_____．

Answer 1

【答案】

【解析】如图，作BF⊥l3，AE⊥l3，

∵∠ACB=90°，

∴∠BCF+∠ACE=90°，

∵∠BCF+∠CFB=90°，

∴∠ACE=∠CBF，

在△ACE和△CBF中， ，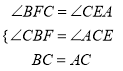

∴△ACE≌△CBF，

∴CE=BF=6，CF=AE=8，

∵l1与l2的距离为2，l2与l3的距离为6，

∴AG=2，BG=EF=CF+CE=14，

∴AB= ，

∵l2∥l3，

∴，

∴DG=CE=，

∴BD=BG-DG=14-=，

∴==，

故答案为： ．