题目内容
【题目】已知:一个正比例函数图象y=2x和一个一次函数y=kx+b的图象交于点P(﹣2,a)且一次函数的图象与y轴的交点Q的纵坐标为4.
(1)求这两个函数的解析式;
(2)在同一坐标系中,分别画出这两个函数的图象;
(3)求△PQO的面积.
【答案】(1) 正比例函数图象y=2,一次函数的解析式为y=4x+4 ;(2)如图;(3) △PQO的面积为4.
【解析】
(1)把点P(-2,a)代入y=2x可得a的值,再把点P和点Q的坐标带入y=kx+b,即可求得;
(2)过原点和点P可画出正比例函数图象y=2x的图像,过点P和点Q可画出一次函数y=kx+b的图象;
(3)以OQ为底利用面积公式求解即可.
解:(1)∵正比例函数y=2x经过点P(-2,a),
∴a=2×(-2)=-4
∴P(-2、-4),
∵一次函数y=kx+b的图象经过点P(-2,-4)且与y轴的交点Q的纵坐标为4,
∴Q(0,4),
∴![]() ,
,
解得
![]()
∴正比例函数图象y=2,一次函数的解析式为y=4x+4.
(2)如图所示,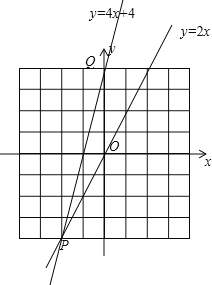
(3)∵P(-2、-4),Q(0,4),
∴S△PQO= ![]()
![]() 4
4 ![]() 2=4,
2=4,
∴△PQO的面积为4.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目