题目内容
 如图,在宽为20米,长为32米的矩形地面上,修筑平行于矩形两边的同样宽的两条互相垂直的道路,余下的部分作为耕地,要使耕地的面积为540平方米,道路的宽应是
如图,在宽为20米,长为32米的矩形地面上,修筑平行于矩形两边的同样宽的两条互相垂直的道路,余下的部分作为耕地,要使耕地的面积为540平方米,道路的宽应是
- A.1米
- B.2米
- C.3米
- D.4米
B
分析:把四块耕地拼到一起正好构成一个矩形,矩形的长和宽分别是(32-x)和(20-x),根据矩形的面积公式,列出关于道路宽的方程求解.
解答:设道路的宽为x米.依题意得:
(32-x)(20-x)=540,
解之得x1=2,x2=50(不合题意舍去)
∴道路宽为2m.
故选B.
点评:本题考查了一元二次方程的应用,关键将四个矩形恰当的方式拼成大矩形列出等量关系.
分析:把四块耕地拼到一起正好构成一个矩形,矩形的长和宽分别是(32-x)和(20-x),根据矩形的面积公式,列出关于道路宽的方程求解.
解答:设道路的宽为x米.依题意得:
(32-x)(20-x)=540,
解之得x1=2,x2=50(不合题意舍去)
∴道路宽为2m.
故选B.
点评:本题考查了一元二次方程的应用,关键将四个矩形恰当的方式拼成大矩形列出等量关系.

练习册系列答案
相关题目
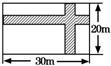 10、如图,在宽为20米,长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米2,则修建的路宽应为( )
10、如图,在宽为20米,长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米2,则修建的路宽应为( )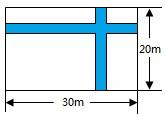 24、如图,在宽为20米、长为30米的矩形地块上修建两条等宽的道路,余下部分种植花草.若种植花草的地块面积为551米2,求修建的路宽.
24、如图,在宽为20米、长为30米的矩形地块上修建两条等宽的道路,余下部分种植花草.若种植花草的地块面积为551米2,求修建的路宽.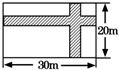 14、如图,在宽为20米、长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米2,则修建的路宽应为
14、如图,在宽为20米、长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米2,则修建的路宽应为
 列方程解应用题
列方程解应用题