题目内容
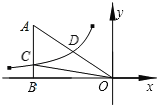
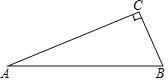
【题目】（问题情境）在△ABC中，AB＝AC，点P为BC所在直线上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D、E，过点C作CF⊥AB，垂足为F．当P在BC边上时（如图1），求证：PD+PE＝CF．
证明思路是：如图2，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD+PE＝CF．（不要证明）
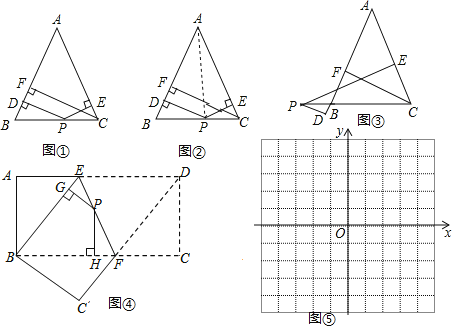
（变式探究）（1）当点P在CB延长线上时，其余条件不变（如图3），试探索PD、PE、CF之间的数量关系并说明理由；
请运用上述解答中所积累的经验和方法完成下列两题：
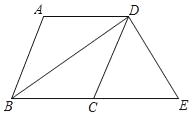
（结论运用）（2）如图4，将长方形ABCD沿EF折叠，使点D落在点B上，点C落在点C′处，点P为折痕EF上的任一点，过点P作PG⊥BE、PH⊥BC，垂足分别为G、H，若AD＝16，CF＝6，求PG+PH的值．
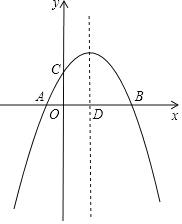
（迁移拓展）（3）在直角坐标系中，直线l1：y＝-
x+8与直线l2：y＝﹣2x+8相交于点A，直线l1、l2与x轴分别交于点B、点C．点P是直线l2上一个动点，若点P到直线l1的距离为2．求点P的坐标．
【答案】【变式探究】证明见解析【结论运用】8【迁移拓展】（﹣1，6），（1，10）
【解析】
【变式探究】
连接AP，同理利用△ABP与△ACP面积之差等于△ABC的面积可以证得；
【结论运用】
过点E作EQ⊥BC，垂足为Q，根据勾股定理和矩形的性质解答即可；
【迁移拓展】
分两种情况，利用结论，求得点P到x轴的距离，再利用待定系数法可求出P的坐标．
变式探究:连接AP，如图3：
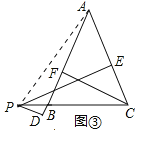
∵PD⊥AB，PE⊥AC，CF⊥AB，且S△ABC＝S△ACP﹣S△ABP，
∴
ABCF＝ACPE﹣ ABPD．
∵AB＝AC，
∴CF＝PD﹣PE；
结论运用:过点E作EQ⊥BC，垂足为Q，如图④，
∵四边形ABCD是长方形，
∴AD＝BC，∠C＝∠ADC＝90°．
∵AD＝16，CF＝6，
∴BF＝BC﹣CF＝AD﹣CF＝5，
由折叠可得：DF＝BF，∠BEF＝∠DEF．
∴DF＝5．
∵∠C＝90°，
∴DC＝
＝8．
∵EQ⊥BC，∠C＝∠ADC＝90°，
∴∠EQC＝90°＝∠C＝∠ADC．
∴四边形EQCD是长方形．
∴EQ＝DC＝4．
∵AD∥BC，
∴∠DEF＝∠EFB．
∵∠BEF＝∠DEF，
∴∠BEF＝∠EFB．
∴BE＝BF，
由问题情境中的结论可得：PG+PH＝EQ．
∴PG+PH＝8．
∴PG+PH的值为8；
迁移拓展:如图，
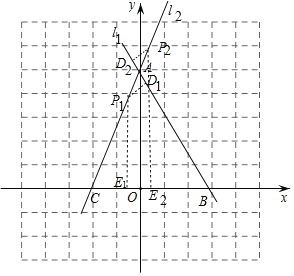
由题意得：A（0，8），B（6，0），C（﹣4，0）
∴AB＝
＝10，BC＝10．
∴AB＝BC，
（1）由结论得：P1D1+P1E1＝OA＝8
∵P1D1＝1＝2，
∴P1E1＝6 即点P1的纵坐标为6
又点P1在直线l2上，
∴y＝2x+8＝6，
∴x＝﹣1，
即点P1的坐标为（﹣1，6）；
（2）由结论得：P2E2﹣P2D2＝OA＝8
∵P2D2＝2，
∴P2E2＝10 点P1的纵坐标为10
又点P1在直线l2上，
∴y＝2x+8＝10，
∴x＝1，
即点P1的坐标为（1，10）
