题目内容

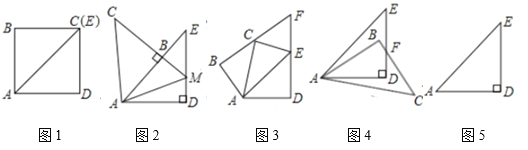
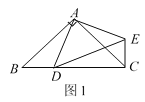
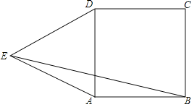
【题目】如图，为正方形外一点，，，则的长为________．

【答案】

【解析】

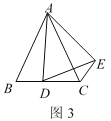
过点E作EF⊥BC于F，交AD于G，作AE的垂直平分线交EF于点O，则点O是△ADE的外心，DG=a，则OE=OD=a，FG=2a，BF=a，在Rt△DEG中，利用勾股定理求出a2，再在Rt△EFB中，利用勾股定理求出BE即可．

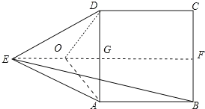
过点E作EF⊥BC于F，交AD于G，作AE的垂直平分线交EF于点O，则点O是△ADE的外心，

∴∠AOD=2∠DEA=90°，OA=OD=OE，

∴OG=DG=AG，设DG=a,则OE=OD=a，FG=2a，BF=a，

在Rt△DEG中，DE2=EG2+DG2，

∴9=(a+a)2+a2，解得a2=，

∴BE====3.

故答案为3.

练习册系列答案
相关题目

【题目】如图，△ABC内接于⊙O，AD是△ABC的中线，AE∥BC，射线BE交AD于点F，交⊙O于点G，点F是BE的中点，连接CE．

（1）求证：四边形ADCE为平行四边形；

（2）若BC=2AB，求证: ．

【题目】阅读情境：在综合实践课上，同学们探究“全等的等腰直角三角形图形变化问题”

如图1，，其中，，此时，点与点重合，

操作探究1:（1）小凡将图1中的两个全等的和按图2方式摆放，点落在上，所在直线交所在直线于点，连结，求证：．

操作探究2:（2）小彬将图1中的绕点按逆时针方向旋转角度，然后，分别延长，，它们相交于点．如图3，在操作中，小彬提出如下问题，请你解答：

①时，求证：为等边三角形；

②当__________时，．（直接回答即可）

操作探究3:（3）小颖将图1中的绕点按顺时针方向旋转角度，线段和相交于点，在操作中，小颖提出如下问题，请你解答：

①如图4，当时，直接写出线段的长为_________．

②如图5，当旋转到点是边的中点时，直接写出线段的长为____________．

【题目】为了促进“足球进校园”活动的开展，某市举行了中学生足球比赛活动现从A，B，C三支获胜足球队中，随机抽取两支球队分别到两所边远地区学校进行交流．

（1）请用列表或画树状图的方法（只选择其中一种），表示出抽到的两支球队的所有可能结果；

（2）求出抽到B队和C队参加交流活动的概率．

【题目】如图1，在平面直角坐标系中，直线与轴、轴分别交于点、，抛物线经过点、，且与轴的另一交点为，连接.

（1）求抛物线的解析式；

（2）点在线段上方的抛物线上，连接、，若和面积满足，求点的坐标；

（3）如图2，为中点，设为线段上一点（不含端点），连接。一动点从出发，沿线段以每秒1个单位的速度运动到，再沿着线段以每秒个单位的速度运动到后停止。当点的坐标是多少时，点在整个运动过程中用时最少？最少时间是几秒？

图1 图2

【题目】在中，为的角平分线.

图1 图2

（1）如图1，，，点在边上，，请直接写出图中所有与相等的线段.

（2）如图2，，如果，求证：.

【题目】在△ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．

（1）如图1，当点D在线段BC上，如果∠BAC=90°，则∠BCE=_______度；

（2）如图2如果∠BAC=60°，则∠BCE=______度；

（3）设∠BAC=，∠BCE=．

①如图3，当点D在线段BC上移动，则之间有怎样的数量关系？请说明理由；

②当点D在直线BC上移动，请直接写出之样的数量关系，不用证明。

【题目】在日历上，我们可以发现其中某些数满足一定的规律，如图是2012年8月份的日历．我们任意选择其中所示的方框部分，将每个方框部分中4个位置上的数交又相乘，再相减，例如：7×13－6×14＝7，17×23－16×24＝7，不难发现，结果都是7．

①请你再选择一个类似的部分试一试，看看是否符合这个规律；

②请你利用整式的运算对以上的规律加以证明．

【题目】无锡市新区某桶装水经营部每天的房租、人员工资等固定成本为250元，每桶水的进价是5元，规定销售单价不得高于12元/桶，也不得低于7元/桶，调查发现日均销售量p（桶）与销售单价x（元）的函数图象如图所示．

（1）求日均销售量p（桶）与销售单价x（元）的函数关系；

（2）若该经营部希望日均获利1350元，那么销售单价是多少？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网