��Ŀ����
����Ŀ���ڡ�ABC�У�AB=AC����D��ֱ��BC��һ�㣨����B��C�غϣ�����ADΪһ����AD���Ҳ�����ADE��ʹAD=AE����DAE=��BAC������CE��
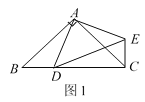
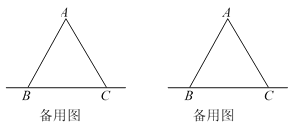
��1����ͼ1������D���߶�BC�ϣ������BAC=90�������BCE=_______�ȣ�
��2����ͼ2�����BAC=60�������BCE=______�ȣ�
��3�����BAC=![]() ����BCE=
����BCE=![]() ��
��
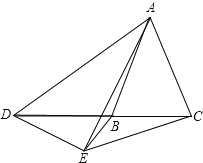
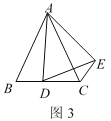
����ͼ3������D���߶�BC���ƶ�����![]() ֮����������������ϵ����˵�����ɣ�
֮����������������ϵ����˵�����ɣ�
�ڵ���D��ֱ��BC���ƶ�����ֱ��д��![]() ֮����������ϵ������֤����
֮����������ϵ������֤����

���𰸡���1��90����2��120�� ��3�� ����+��=180������+��=180������=��
��������
���⣨1����������֤����ABD�ա�ACE���ɵ���ABD=��ACE=45�㣬���������������ACB=45�㣬�������BCE=90�㣻
��2��ͬ��1����֤����ABD=��ACE������ABC���ɵ��������ε����ʿ������ACD���Ӷ��������BCE��
��3����ͬ��1����֤����ABD=��ACE������ABC���ɵ��������ε����ʿ������ACD=��ABC=![]() ���Ӷ��������BCE��������ͬ����
���Ӷ��������BCE��������ͬ����
�����������1���ߡ�DAE=��BAC��
���BAD=��CAE��
����ABD����ACE��
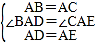
���ABD�ա�ACE��SAS����
���ABD=��ACE��
��AB=AC����BAC=90�㣬
���ABD=��ACB=45�㣬
���BCE=��ACB+��ACE=45��+45��=90�㣬
��2���ߡ�DAE=��BAC��
���BAD=��CAE��
����ABD����ACE��
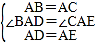
���ABD�ա�ACE��SAS����
���ABD=��ACE��
��AB=AC����BAC=60�㣬
���ABD=��ACB=![]() =60�㣬
=60�㣬
���BCE=��ACB+��ACE=60��+60��=120�㣻
��3���١ߡ�DAE=��BAC��
���BAD=��CAE��
����ABD����ACE��
���ABD�ա�ACE��SAS����
���ABD=��ACE��
��AB=AC����BAC=����
���ABD=��ACB=![]() ��
��
���BCE=��ACB+��ACE=2��ACB=180��-����
����ͼ������D������BC��ʱ����+��=180��
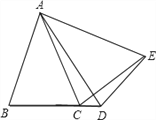
��ͼ������D������BC�ķ����ӳ�����ʱ����=�£�